Résumé : le tapis de Sierpińsky est un objet mathématique fascinant qui offre des particularités intéressantes. Il peut être défini de très nombreuses façons et, même à partir du triangle de Pascal.
Mots-clés : coefficients binomiaux, triangle de Pascal, fractals.
La construction géométrique du triangle de Sierpińsky s’effectue comme suit : on part d’un triangle plein dans le plan, puis on applique un schéma répétitif d’opérations ; on prend les milieux de chaque côté ; ceux-ci définissent quatre triangles, on ôte celui qui est au centre ; on répète cette opération avec les trois autres triangles.
Le triangle de Sierpińsky est défini comme l’ensemble des points qui sont conservés lorsque le processus est répété indéfiniment.
Le tapis de Sierpińsky est défini de façon similaire. On part cette fois d’un carré et on divise les côtés en trois segments égaux.
Le triangle de Pascal est un tableau de nombres de forme triangulaire bien connu. Bien qu’il ne l’ait pas découvert, ce triangle porte son nom (On a retrouvé une publication chinoise datant de 1303 ). Il est défini à partir des coefficients des polynômes de degré n. Ainsi, la ligne n est donnée par a0,a1,…,an où
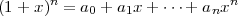
On peut représenter le triangle de Pascal en le colorant en noir et blanc. Dans l’exemple ci-dessous, les nombres pairs sont en blanc et les impairs en noir. Cette représentation peut être faite également en prenant les critères de divibilité par 3,4,5,…
Le problème consiste à représenter les triangles de Pascal et de Sierpińsky ainsi que le tapis de Sierpińsky.
Cet exercice est tiré du livre Chaos and Fractals de Peitgen, Jürgens et Saupe publié chez Springer-Verlag, 1992. On y trouve également quelques informations sur Waclaw Sierpińsky (1882-1969). Il était professeur à Lvov1 et à Varsovie. Il était un des mathématiciens les plus influents de son époque en Pologne et bénéficiait d’une réputation mondiale. Un des cratères de la lune porte son nom. Il a écrit Sur une courbe dont tout point est un point de ramification, C. R. Acad. Paris (1915) et Sur une courbe cantorienne qui contient une image biunivoque et continue de toute courbe donnée, C. R. Acad. Paris (1916).
La façon la plus simple de représenter le triangle de Sierpińsky est de commencer par la fin : la représentation du triangle de Pascal. Le calcul des différentes lignes du triangle de Pascal peut se faire à partir de l’évaluation des expressions :
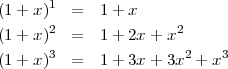
En calculant de façon plus générale, on peut déduire une autre façon de calculer ces coefficients appelés coefficients binomiaux :
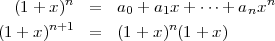
Avec la formule de calcul des coefficients binomiaux, on peut calculer plus facilement les grandes valeurs des coefficients :
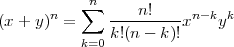
Pour déterminer la parité des coefficients du triangle de pascal, il suffit de considérer le reste de la division euclidienne par 2. Il est très intéressant de vérifier que les calculs peuvent se faire sur les restes et non sur les coefficients. De la sorte, il n’y a plus de grandes valeurs difficiles à calculer.
Pour obtenir une première version du triangle de Sierpińsky, il suffit donc de colorer le triangle de Pascal suivant les restes de la division des coefficients par 2.
Pour dessiner le triangle de Sierpińsky, il est conseillé de prendre un triangle équilatéral et de le représenter (on appelle cette courbe, initiateur). La première étape consiste à remplacer chaque côté par la courbe ci-dessous2 (on l’appelle générateur). Puis, à chaque nouvelle étape, on remplace chaque segment par ce même générateur.
La solution actuellement proposée est donnée par les fichiers MatLab : DemoSierp.m, SierpDemo.m, TapisDemo.m, PascDemo.m, SierpRand.m, tapis.m et sierp2.m.