Résumé : en observant un point sur la roue d’un vélo, on aperçoit une courbe aux propriétés particulièrement intéressantes. Cette courbe, appelée cycloïde, intéresse également les physiciens : des pendules précis, des billes qui se rejoignent toujours au même point, des chemins plus rapides entre deux points, toutes ces applications font ressortir les qualités de cette courbe.
Mots-clés : trajectoire, cynétique, intégration, enveloppe, réfraction, vitesse.
Sur le pneu de la roue d’une bicyclette, on a marqué à la craie un point qui soit bien visible. Quelle est la courbe parcourue par ce point lorsque la bicyclette roule sur la route ?
Quelle est la longueur d’un arc de cette courbe (ou également, la longueur de la trajectoire du point lorsque la roue a fait un tour complet) ? De la même façon, quelle est l’aire de la surface délimitée par un arc et la droite sur laquelle la roue a roulé ?
Cette courbe s’appelle cycloïde et possède de nombreuses propriétés curieuses. Les scientifiques du XVIIIe ont commencé à l’étudier avec délice et à organiser de véritables batailles pour savoir qui avait trouvé le premier telle ou telle propriété. Huygens, les frères Bernoulli, Newton, De l’Hospital ont échangé leurs observations sur la cycloïde.
Essayez d’en redécouvrir une due à Huygens (il fut le premier constructeur sérieux d’horloges à balancier ainsi qu’un physicien et mathématicien). Construisez un pendule dont les côtés sont deux demi-arcs de la cycloïde comme décrit ci-dessous. Quelle est la période du pendule, que peut-on en déduire ?
Orientez une cycloïde vers le haut comme dans la figure ci-dessous. Considérez deux billes placées en deux points quelconques sur la cycloïde. A quel endroit vont-elles se rejoindre ?
Supposez que vous ayez un fil de fer et une perle de collier. On enfile la perle d’un côté du fil et on la fait glisser jusqu’à l’autre extrêmité. Quelle forme faut-il donner au fil de fer pour que la perle mette le moins de temps possible pour arriver à destination ? Le chemin le plus court entre deux points ne serait-il pas le plus rapide ?
Cet exercice est tiré du livre Aventures mathématiques de Miguel de Guzmán publié aux Presses polytechniques et universitaires romandes, 1990.
Avant toute chose, essayez de déterminer l’équation de la cycloïde, puis, de la représenter. Dessinez un cercle et marquez un point P quelconque sur ce cercle, puis faites tourner le cercle d’un angle α et déterminer P′ la position de P en fonction de cet angle. On obtient alors des équations en coordonnées paramétriques pour x et y : x = φ(t) et y = ψ(t). Rappel : la longueur d’un arc de cercle est donné par rα.
Pour calculer la longueur d’un arc de la cycloïde, procédez de deux façons : en additionnant des longueurs de segments de droites pour obtenir une approximation et en la déterminant analytiquement. Rappel : pour calculer la longueur d’un arc, on calcule l’intégrale suivante :
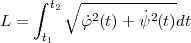 | (5.1) |
Pour déterminer l’aire de la surface délimitée par un arc et la droite, le même processus peut être engagé. On utilisera la méthode des trapèzes ou de Simpson pour obtenir une approximation, puis on résoudra l’intégrale suivante :
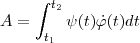 | (5.2) |
Pour construire le pendule de Huygens, on part d’une cycloïde classique, puis on détermine les normales aux points qui constituent la cycloïde. Dans un deuxième temps, on construit l’enveloppe de ces droites en considérant la courbe qui leur est tangente. Il suffit de calculer la dérivée de l’équation des normales par rapport à α. L’équation des points de l’enveloppe est alors celle des points appartenant aux normales et à leurs dérivées.
On utilisera la loi sur la chute des corps pour calculer la vitesse et le temps de
déplacement de la bille dans la cycloïde.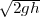 
= vα où h est la différence
d’altitude entre deux points de la cycloïde inversée. Comme la longueur d’un
segment est également la vitesse multipliée par le temps, on peut intégrer la
longueur sur la vitesse. De ce résultat on peut déduire la propriété du
pendule de Huygens et répondre à la question sur l’endroit où les billes se
rejoignent.
La loi de la réfraction (demander au maître de physique en cas de doute)
permet de construire le chemin qui donne le temps minimal du parcours de la
lumière dans un milieu tel que la vitesse varie constamment. On se rappelle
encore une fois, que quel que soit le chemin emprunté par la perle, quand elle
aura descendu h, sa vitesse sera de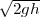 
. Par le principe de Fermat, on sait que
la lumière voyage d’un point à un autre dans le temps le plus petit possible. Nous
savons aussi que la vitesse de la lumière varie, selon le milieu où elle voyage.
C’est le phénomène de la réfraction. Si la lumière voyage à des vitesses
v1 et v2 dans deux milieux différents, la loi de la réfraction nous dit
que
 | (5.3) |
En imaginant un milieu formé par des couches I1, I2,..., In horizontales et fines tel que la vitesse de la lumière dans chacune d’elles soit v1, v2,...., vn, alors un rayon, qui partirait de A et arriverait en B, suivrait une trajectoire comme celle de la figure ci-dessous de façon que
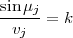 | (5.4) |
Ce chemin serait le chemin du temps minimal pour aller de A à B aux vitesses
indiquées. Dans le cas de la cycloïde, on connaît la vitesse en descendant de h.
Ainsi, le chemin qui donnera le temps minimal sera le chemin que suit un rayon
de lumière dans un milieu tel que la vitesse de la lumière varie constamment en
descendant de h et soit précisément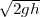 
. Or, pour ce chemin, on peut déjà
vérifier
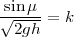 | (5.5) |
Comme la courbe recherchée doit satisfaire cette équation, il suffit de calculer tanμ = dx∕dy pour la cycloïde et de déterminer μ. On pourra vérifier alors si la cycloïde vérifie la propriété recherchée.
La solution actuellement proposée est donnée par les fichiers MatLab : cyclo.m, cycloD.m, cycloD.mat, tautochrone.m, cycloDemo.m et cyclo.m.