Résumé : la thermodynamique est l’étude des propriétés statistiques des gaz ; elle traite de la température, de la pression, du volume et de l’entropie. Quelles analogies peut-on trouver avec une courbe ? Qu’est-ce que l’entropie d’une courbe ?
Mots-clés : physique, thermodynamique, dimension, température, pression, volume, entropie, spirale de Cornu.
L’exercice s’inspire de l’article La physique des courbes, Une étude thermodynamique des courbes définies par des suites extrait de Visions géométriques de Ian Stewart, Bibliothèque pour la Science, Diffusion Belin, Paris, 1993.
Pour introduire son sujet, Ian Stewart imagine un architecte construisant un parking de supermarché original : il s’agit d’un système complexe de spirales et de fioritures zigzaguant de-ci de-là, mais pas véritablement au hasard. Le graphique est donné ci-dessous.
L’article fait également référence aux travaux de Michel Mendès France et Michel Dekking. Les auteurs tentent de trouver une analogie entre la thermodynamique et les courbes. Les courbes sont très simples à constuire ; elles ont en revanche des propriétés intéressantes.
Michel Mendès France affirme dans ses recherches qu’une courbe peut avoir une dimension supérieure à un, une entropie, une température et un volume. Il définit ces quantités en utilisant une analogie avec la thermodynamique.
La dimension d’une courbe est mieux connue depuis l’essor des fractales. Mais Michel Mendès France l’explique comme suit : une courbe est dite linéaire si sa dimension est 1 et « superficielle » si sa dimension est supérieure à 1. Par exemple, une spirale logarithmique est linéaire (r = eθ) alors qu’une spirale d’Archimède est superficielle (de dimension 2. L’équation est : r = θ). Michel Mendès France et Michel Dekking découvrirent une mine de courbes superficielles, construites avec des polygones infinis.
La définition de la dimension d’une courbe selon Michel Mendès France est donnée comme suit : entourons une courbe par une région de largeur 2W et appelons A l’aire de la partie de cette région située à l’intérieur du cercle de rayon R, de centre arbitraire fixe. La dimension de la courbe est la limite, si elle existe, de log A∕log R lorsque R →∞ et W → 0.
Pour expliquer les polygones infinis, on remarque que chaque nombre x détermine une direction du plan orienté muni d’un axe horizontal, celle qui forme avec cet axe, un angle orienté de 2πx radians, ou 360x degrés. Les valeurs de x comprises entre 0 et 1 déterminent toutes les directions possibles et, qui plus est, ajouter un nombre entier à x ne change pas la direction. La direction ne dépend, dans l’écriture décimale de x que de la partie après la virgule, dite partie fractionnaire x x( mod 1).
Ian Stewart prend ensuite comme exemple la suite : x0,x1,x2,…, avec
xn = sin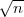
. On construit alors la courbe polygonale G(x) comme suit : d’un
point de départ choisi, on trace un segment de longueur fixée dans la direction
correspondant à x0. De là, on trace un nouveau segment de même longueur dans
la direction correspondant à x1. On recommence avec x2 et ainsi de suite, en
utilisant toute la suite infinie. La courbe obtenue est donnée ci-dessous. Il est clair
que cette courbe se poursuit notamment vers la droite, décrivant des doubles
boucles de plus en plus grandes. Les boucles croissent lentement et restent
séparées les unes des autres de sorte que la courbe semble plus linéaire que
superficielle.
Chaque suite x = (xn) conduit à une courbe G(x) différente. C’est une courbe de ce type qui a été utilisée par l’architecte pour dessiner le parking. On peut facilement les dessiner sur une feuille de papier mais, s’il faut répéter de nombreuses fois les étapes, un ordinateur rendra de grands services.
M. Dekking et M. Mendès France ont caractérisé les suites x conduisant à des courbes superficielles : ils ont prouvé que la suite x est « équidistribuée modulo 1 » si et seulement si toutes les courbes G(mx) sont superficielles pour tous les entiers m non nuls. Une suite est équidistribuée modulo 1 si et seulement si les directions correspondantes sont également distribuées sur un cercle.
Une famille particulière de suites est véritablement passionnante : xn = an2 où a est constant. Ce qui est remarquable dans ces suites provient du choix de a : avec des valeurs différentes on obtient une grande variété de courbes.
Il est toujours conseillé de commencer par des cas simples : on peut prendre a = 1∕N où N est un entier. Les courbes correspondantes ont une structure spiralée simple rappelant les spirales de Cornu utilisées en optique pour les problèmes de diffraction.
Les analogies avec la thermodynamique sont intéressantes : la loi des gaz parfaits énonce que PV = RT où P est la pression, T, la température, V le volume et R une constante. Soit G une courbe plane de longueur finie. Une droite K arbitraire du plan, rencontre G en un nombre fini nk de points. En thermodynamique, l’entropie d’un système est défini par :
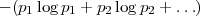
où p1 est la probabilité de rencontrer le système dans l’état n. Pour les courbes nous noterons pn la probabilité qu’une droite K, choisie au hasard, rencontre G dans l’état n, donc la pn est la probabilité pour que nk = n. L’entropie d’une courbe G est alors, si l est la longueur de la courbe G et h celle de l’enveloppe convexe (la plus petite courbe qui la contienne) :
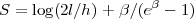
où
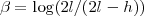
En thermodynamique traditionnelle, la température T est définie comme l’inverse de β, de sorte que, par définition :
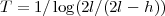
Poursuivant l’analogie, le volume V est défini comme sa longueur : V = l et la pression P par l’inverse h-1 de la longueur de l’enveloppe.
Il faut définir un algorithme général permettant de construire n’importe quelle courbe G à partir d’une suite xn : on choisit un point de départ (sx,sy) et un facteur d’échelle sf permettant de zoomer sur le graphique.
A chaque étape on calcule : x′ = x + sf cos(2πxn), y′ = y + sf sin(2πxn), puis x = x′ et y = y′. On représente alors le segment qui relie (x;y) à (x′;y′).
Ian Stewart pose également un problème intéressant : à partir d’une courbe G de la forme G(an2), peut-on retrouver a ? Il suggère alors de commencer par étudier les raisons des fioritures. En prenant comme cas particulier a = 1∕N, N étant un grand nombre entier. Considérons la n-ième phase, c’est-à-dire l’angle entre le n-ième et le (n + 1)-ième côté du polygone G(n2∕N). Sa mesure est ((n + 1)2 - n2)2π∕N soit (2n + 1)2π∕N. Lorsque n est petit devant N la différence de phase est également petite, de sorte que les côtés ont presque la même direction, et la courbe est peu incurvée. Lorsque n augmente, la différence de phase atteint le voisinage de π∕2 et les côtés s’enroulent, formant une sorte de tache. Quand n approche la valeur N∕4, chaque côté recouvre à peu près son prédécesseur. Lorsqu n dépasse N∕4 la courbe commence à se dérouler et, quand n approche la valeur N∕2, la fioriture est achevée et la courbe est presque rectiligne. Après quoi elle s’enroulera de nouveau pour former une autre fioriture. Après N étapes, l’orientation se répète. Il y a quatre cas selon que N est de la forme 4m, 4m + 1, 4m + 2 ou 4m + 3 (N mod 4).
Un autre cas simple apparaît lorsque a = p∕q, avec p et q entiers premiers entre eux (a est un nombre rationnel). Ces nombres conduisent à des structures spiralées périodiques analogues au cas où a était égal à 1∕N.
La solution actuellement proposée est donnée par les fichiers MatLab : lochness.m.