Résumé : le tracé d’un crayon qui suit la rotation d’un cercle sur un autre est connu des jeunes enfants. Les fabricants de jouets leur ont imaginé un outil permettant de représenter de fort belles courbes avec le spirographe. Les mathématiques et l’informatique permettent de les reproduire à volonté.
Mots-clés : courbe paramétrique, trigonométrie, cercle.
L’exercice s’inspire du livre Mathematica in Action de Stan Wagon, Springer, Berlin, 1008.
Le spirographe est un ver marin construisant dans le sable vaseux un tube souple, d’où sort un panache branchial en hélice (de spira « spire » et graphis « crayon »). En l’observant, les mathématiciens et les zoologues ont pu inspirer les fabricants de jeux qui proposent des outils combinant habilement des disques crantés et des couleurs pour obtenir des figures simples et complexes.
Pour rester dans le domaine de la zoologie, existe-t-il une courbe permettant de représenter un papillon ? Les mathématiciens ont trouvé de tels courbes ; souvent ils les qualifient de paramétriques (en modifiant très légèrement des paramètres, on peut obtenir des courbes totalement différentes).
Un exemple de courbe paramétrique est donné par le cercle : lorsque l’on
demande à un étudiant de représenter un cercle avec un ordinateur (capable de
tirer des traits), il choisit souvent l’expression : y = ±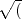
r2 -x2). Celle-ci contient
un petite ambiguïté puisqu’il faut représenter la courbe en deux parties (une fois
la partie négative et une fois la partie positive). Si l’on prend en revanche
l’expression (pourtant bien connue) x = r cost,y = r sint, avec t 
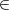[0;2π], le
résultat est bien meilleur (près de 0 et près de π, les points ont le même
espacement angulaire).
En combinant adroitement les fonctions sin(t) et cos(t), on peut obtenir des courbes très spectaculaires. Pour approcher la représentation du papillon, on peut considérer l’expression suivante :
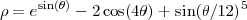
Norton Starr (du Amherst College) propose une piste intéressante pour représenter des courbes dérivées du simple mouvement circulaire. D’abord, il multiplie par un rayon variable de la forme 2 + 1∕2sin(at), ce qui provoque une oscillation entre 1.5 et 2.5 avec une vitesse d’oscillation dépendant de a. Dans le même temps, il modifie l’équation du cercle (cos(t);sin(t) de sorte que le mouvement avance et recule ; ceci est réalisé par (cos(t + sin(bt)∕c);sin(t + sin(bt)∕c)) ; le terme sin à l’intérieur des parenthèses a pour effet de faire osciller la direction angulaire d’avant vers l’arrière avec une vitesse et une amplitude dépendant de b etc.
Des cercles qui tournent sur des cercles qui eux-mêmes tournent sur des cercles conduisent vers des courbes intéressantes. Cette approche, proposée par Farri, est légèrement différente du spirographe dans le sens que les centres des cercles se trouvent sur les bords des cercles précédents. On peut imaginer un cercle tournant à la vitesse de 1 radian à la seconde, un deuxième cercle plus petit dont le centre est sur le bord du premier et tournant 7 fois plus rapidement que le premier et un troisième cercle encore plus petit tournant 17 fois plus rapidement que le premier dans la direction opposée. Maintenant, on peut imaginer le lieu du point situé au départ au pôle nord sur le troisième cercle. Toute cette activité peut se résumer par la forme paramétrique suivante :
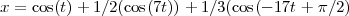
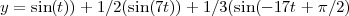
On obtient alors :
En modifiant les rayons, les vitesses et les positions relatives on obtient des courbes fort différentes :
Cet exercice est relativement simple lorsque l’on dispose d’un ordinateur (ou d’une calculatrice graphique évoluée). Il faut calculer les coordonnées des points définis par les équations paramétriques, puis les relier.
Les logiciels qui permettent les animations sont très utiles : ils peuvent rendre le graphique plus explicite.
Pour passer de polaire à cartésien, il est utile de connaître les formules de transformation : x = ρcos(θ), y = ρsin(θ)).
La solution actuellement proposée est donnée par les fichiers MatLab : epicycle.m, starr.m, demofarri.m, demostarr.m et papillon.m.