Résumé : calculer de façon exacte les dynamiques entourant un système aussi complexe que le feu requiert une simulation poussée. Or une approximation existe permettant de représenter un feu de façon extrêmement réaliste et sans difficulté (si l’on dispose d’un ordinateur). Encore un exemple d’algorithme simple permettant de modéliser un comportement complexe.
Mots-clés : modélisation, flamme, feu.
L’exercice s’inspire du mode d’emploi de logiciels graphiques et d’articles sur le web.
Lorsque l’on observe les effets spéciaux au cinéma ou sur Internet on découvre qu’il est possible de simuler les flammes de façon très réaliste. Il s’agit fondamentalement d’une approximation de la réalité, car calculer de façon exacte les dynamiques entourant un système aussi complexe que le feu requiert une simulation poussée (et difficilement réalisable en temps réel sur des ordinateurs personnels).
En fait, comme toujours, il n’y a rien de compliqué. Le tout est de bien observer l’effet pour en tirer un algorithme. Le premier à l’avoir fait avec succès fut un codeur espagnol (dont on a perdu l’adresse).
Il avait remarqué que plus on s’éloigne du foyer du feu, plus la flamme est foncée, tout en gardant le même motif. La couleur d’un point de la flamme (si on la décompose en une multitude de points) dépend de la couleur des points qui se trouvent en dessous de lui. On remarque aussi que le feu tend à s’estomper au fur et à mesure qu’il quitte le « foyer ». Les flammes ne sont pas uniformes, et sont constamment nourries par l’apport d’une source de chaleur.
Le simulateur espagnol était donc arrivé à la conclusion que pour calculer la couleur, la formule idéale serait :
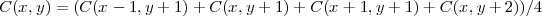
Il faut bien générer les couleurs à la base de la flamme, car si on part d’un écran noir, la moyenne des points, donnera 0 à n’importe quelle position.
Pour créer un foyer, on va donc afficher des points de couleur la plus vive à des postions aléatoires en bas de l’écran. La palette sera donc un dégradé du jaune au rouge foncé. Plus on monte, et plus les points sont foncés.
Pour donner une apparence réaliste au brasier, il faudra que la palette de couleurs soit constituée de tons formant un dégradé de couleurs chaudes. Pour une flamme, il faudra des tons de jaune, d’orange et de blanc. Ce type de problème convient parfaitement à une palette de 256 couleurs (8 bits). Il suffit de créer un dégradé de jaune qui donne sur le rouge, puis finalement le noir. De cette façon le feu aura une apparence classique, mais rien n’empêche la création de feu vert, bleu ou mauve.
Les flammes doivent naturellement perdre de l’intensité. L’algorithme se sert de la moyenne des pixels environnant comme indiqué dans l’énoncé. On peut éventuellement demander de refroidir plus rapidement la flamme en décrémentant cette moyenne.
Si on applique l’algorithme tel quel, le feu s’estompera très rapidement, faute d’apport de pixels « chauds ». Dans l’effet traditionnel, on ajoute une ligne au bas de l’écran, que l’on remplit de pixels ayant une valeur aléatoire élevée (donc près du blanc) à chaque trame. Cette rangée de pixels vient garder le feu en vie. Encore une fois, rien n’empêche d’utiliser autre chose que la norme, comme par exemple un cercle, un rectangle, etc.
Une énorme difficulté surgit lorsque l’on utilise les langages interprétés et, en particulier, les boucles. Or pour résoudre ce problème, on est tenté d’utiliser des boucles. Si l’on utilise des matrices, le temps de calcul est considérablement diminué et le réalisme en est immédiatement amélioré.
La solution actuellement proposée est donnée par les fichiers MatLab : demofeu.m.