Résumé : l’ordinateur permet de réinventer le jeu de billard en lui donnant des formes exotiques : circulaires, elliptiques, en étoile, etc. La question qui se pose reste toutefois : dans quelle direction tirer une première boule en visant une bande pour atteindre une deuxième balle à coup sûr ?
Mots-clés : réflexion, dérivation, zéro d’une fonction.
L’exercice s’inspire du livre Solving Problems in Scientific Computing Using Maple and MatLab de Walter Ganter et Jiří Hřebíček chez Springer-Verlag, Berlin, 1993. On trouvera également des informations extrêmement détaillées dans Amateur Physics for the Amateur Pool Player de Ron Shepard (sur Internet).
L’origine du jeu du billard est inconnue. On trouve en 1674 un premier règlement du jeu imprimé en anglais. Le XVIIIe siècle voit se développer de nombreuses formes de billard en Europe. La table était constituée d’une simple planche, d’un tapis vert (l’herbe du début) et de bandes de bois. On fixa par la suite des tissus sur les bords pour améliorer le rebond des billes. Un capitaine d’infanterie eut l’idée géniale de fixer un bout de cuir sur une des extrémités de la crosse. Dès 1800, on voit l’abandon des tables en bois au profit du marbre et de l’ardoise. L’invention du caoutchouc permet l’amélioration du renvoi sur les bandes... Depuis tout s’embrouille : on parle de carambole, de pool, snooker, billard anglais.
Le jeu du billard intéresse également le physicien et le mathématicien : « soient une table de billard (non nécessairement rectangulaire) et deux boules qui y sont déposées, dans quelle direction doit-on frapper la première boule pour qu’en rebondissant sur une bande de la table, elle touche ensuite la deuxième boule ? ». Le problème a une solution pour n’importe quelle forme de billard pour autant que la courbe mathématique qui décrit la table soit dérivable une fois.
Pour obtenir un modèle physique, il est conseillé de faire référence au texte mentionné au début de cet énoncé.
La solution du problème peut être divisée en deux étapes principales. Premièrement, la trajectoire de la boule réfléchie est trouvée. Deuxièmement, le point sur la bande est recherché afin que la deuxième balle soit sur la trajectoire.
La première partie peut être résolue par une généralisation du problème du miroir (l’angle d’impact est égal à l’angle de réflexion).
Dans la deuxième partie on calcule la distance entre la trajectoire réfléchie et la position de la deuxième boule. Cette distance est fonction du point d’impact (le problème est résolu lorsque la distance vaut 0).
Pour commencer, on construit un point M comme un point miroir de P en utilisant la droite l comme axe de symétrie. La droite l′ reliant les points M et Q coupe la droite l au point T. Le chemin recherché passe par le point T. Du point P on doit viser dans la direction du point T pour atteindre la boule située au point Q. On peut décrire cette droite implicitement :
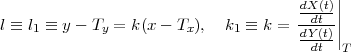
où
![T ≡ [Tx,Ty] = [X (t),Y (t)]](am341x.png)
et où Tx, Ty sont les coordonnées du point commun sur la bande du billard et k est la dérivée de la fonction définissant le bord à ce point. La boule frappant le bord est réfléchie par la droite. Pour trouver l’image miroir de la position d’une boule on utilise l comme droite miroir. La solution du billard généralisé est montrée dans la figure ci-dessous. On peut viser la boule située au point P vers un point T sur le bord du billard. On utilise une droite l1, tangente au bord par T, pour trouver le point M, l’image miroir de P. l2 est le segment de droite reliant le point P et le point M. l1 est perpendiculaire à l2 et coupe l2 au point milieu C.
Si le point M est connu, il est alors possible de dessiner un segment de droite l3 par les points M et Q et un rayon l4 (issu de M et passant par T). La boule située au point P doit se déplacer le long de ce rayon après réflexion. Maintenant il est possible de calculer la distance d2 entre le point Q et le rayon l4. Si la distance est égale à zéro, alors la position de la seconde boule se trouve sur la trajectoire de la première boule après réflexion. Ainsi, les boules se heurtent. Une deuxième possibilité est de calculer la distance d1 entre les points T et W, l’intersecton entre les droites l1 et l3. Pour toucher la boule située au point Q la distance doit également être égale à zéro, puisque dans ce cas T eet W coïncident. Le calcul de la distance d1 est plus aisée que celle de d2.
Pour la solution analytique, on considère ce même schéma en décrivant toutes les droites de la même façon. Une droite peut être décrite par les coordonnées d’un point s’y trouvant et une direciton. La droite l1 a été décrite plus haut. Les autres droites sont données par :
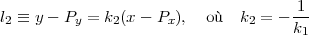
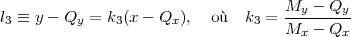
La façon la plus simple de calculer les coordonnées du point M est de trouver le point C d’intersection des droites l1 et l2, et d’utiliser la condition du miroir
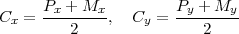
Ainsi, il est possible de calculer les coordonnées du point W qui est à l’intersection des droites l1 et l3, et de déterminer la distance d’erreur lors de la visée d1
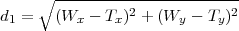
En utilisant ces équations, on peut calculer d1 comme une fonction des coordonnées des positions des boules , de la courbe décrivant le bord du billard et sa permière dérivée
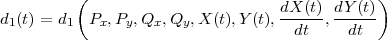
La solution actuellement proposée est donnée par les fichiers MatLab : billard.m, ellipse.m, etoile.m, pointb.m, rond.m, rosace.m, spirale.m, trace.m, trajt.m et trajtt.m.