Chapitre 89
Passer l’éponge

Résumé : Karl Menger a eu l’idée originale de décrire mathématiquement une éponge dont le volume est nul et l’aire est infinie. Elle est obtenue en partant d’un cube dont on enlève une infinité d’éléments.

Mots-clés : auto-similarité, fractal, cube.

Enoncé

L’exercice s’inspire du projet du Dr. Jeannine Mosely intitulé ”Business Card Menger Sponge Project”. Il consiste à fabriquer une approximation de l’éponge de Menger de profondeur 3 avec 66’048 cartes de visite. L’éponge terminée mesurera 140cm de côté et pèsera 70kg (voir le site Internet : http://world.std.com/~j9/sponge/index.html).

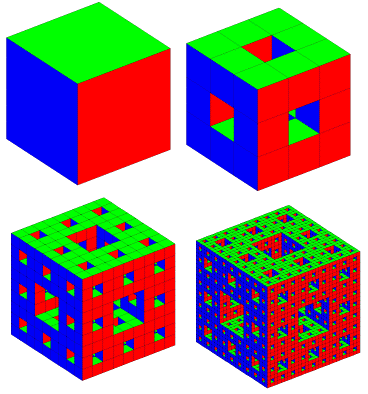
Pour commencer, on prend un cube. Il s’agit de l’éponge de Menger de niveau (ou profondeur) zéro. Pour construire l’éponge de Menger de niveau un, on découpe le cube de niveau 0 en 27 cubes (3 × 3 × 3). Ensuite on ôte le cube qui se trouve au centre et les six autres cubes qui touchent le cube central. Il en reste donc vingt.

Pour passer au niveau deux, on part du niveau un : on considère les cubes restant et on les découpe en 27 cubes ; on ôte à chacun d’eux le cube central et les six cubes adjacents. Il en reste quatre cents. Pour le niveau trois, on procède de même et on obtient 8000 cubes. Le processus se poursuit à l’infini : le volume tend vers zéro et l’aire augmente indéfiniment.

L’aspect fractal apparaît immédiatement. On peut comparer l’éponge de Menger avec le tapis de Sierpińsky. Karl Menger (13.1.1902, Vienne - 5.10.1985, Chicago) est un mathématicien autrichien. Il s’est intéressé à la géométrie hyperbolique et probabiliste et aux fonctions algébriques.

Soit N_n, le nombre de cubes remplis, L_n, la longueur du côté du trou et V _n, le volume fractionnaire au niveau n, alors

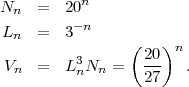
La dimension fractale est :

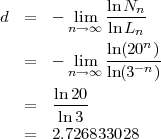
Le but du problème est de représenter l’éponge de Menger au moins aux premiers niveaux. Passer l’éponge c’est oublier, pardonner. En référence à l’éponge imbibée d’eau qu’on passe sur un objet qu’on veut nettoyer ou effacer :

Indications

Même si la récursivité n’est pas la plus performante, il est conseillé de l’utiliser pour résoudre ce problème.

L’algorithme suivant est relativement performant :

• on définit de façon globale une matrice de dimension 3ⁿ × 3ⁿ × 3ⁿ, où n est le niveau ;
• on appelle ensuite une fonction (ou sous-programme) vingt fois, pour chaque cube visible, de façon récursive en indiquant :
  • le déplacement suivant les trois dimensions de la matrice (ligne, colonne et hauteur) pour chaque cube ; 0, 1 ou 2 suivant la position dans la grille (les décalages sont donnés par couche ; les cases vides indiquent les cubes ôtés) :

    (1,1)2,0,0	(1,2)2,1,0	(1,3)2,2,0
    (2,1)1,0,0	(2,2)	(2,3)1,2,0
    (3,1)0,0,0	(3,2)0,1,0	(3,3)0,2,0
    (4,1)2,0,1	(4,2)	(4,3)2,2,1
    (5,1)	(5,2)	(5,3)
    (6,1)0,0,1	(6,2)	(6,3)0,2,1
    (7,1)2,0,2	(7,2)2,1,2	(7,3)2,2,2
    (8,1)1,0,2	(8,2)	(8,3)1,2,2
    (9,1)0,0,2	(9,2)0,1,2	(9,3)0,2,2
    (10,1)

  • le décalage de chaque cube suivant le niveau (ligne, colonne et hauteur) ; il est calculé en additionnant le décalage donné par le niveau précédent au décalage local multiplié par 3ⁿ où n est le niveau de récursivité. Au niveau 2, le décalage entre chaque cube est de 3 = 3¹, au niveau 3 il est de 9 = 3², etc. Ce décalage est multiplié par la position dans la matrice (la case (2,2,1) doit être décalée de 2 fois le décalage pour la ligne, 2 fois le décalage pour la colonne et 1 fois le décalage pour la hauteur) ;
  • la récursivité se termine lorsque n vaut 1. On place alors un 1 dans la matrice.
• on parcourt la matrice construite récursivement suivant le modèle ci-dessus. Si un cube doit être représenté, on le dessine en le décalant suivant l’indice donné par la matrice : si la case (0,1,0) doit être représentée, on dessine un cube en le décalant de 1 suivant les y.

Solutions

La solution actuellement proposée est donnée par les fichiers MatLab : mengerDemo.m et menger.m.