Résumé : L’ensemble de Mandelbrot est une fractale dont la description est extrêmement simple. C’est l’ensemble des points du plan complexe pour lesquels la suite zn+1 = zn2 + c,z0 = 0, ne diverge pas. De nombreuses représentations graphiques – une infinité théoriquement – de cet ensemble sont disséminées sur tous les sites et dans tous les ouvrages traitant de fractales. L’ordinateur est le seul moyen fiable et suffisamment performant pour le représenter.
Mots-clés : fractale, nombre complexe.
Benoît Mandelbrot a donné une conférence à Genève, le 15 mars 2007 intitulée « Les fractales : une randonnée de l’art à l’art, à travers les mathématiques et les sciences ». Ce fut l’occasion de rencontrer ce mathématicien que l’on côtoie virtuellement depuis des années lorsque l’on est passionné par les mathématiques et l’informatique. L’ensemble auquel il a donné son nom et les fractales ont toujours intéressé les informaticiens. Les capacités de calcul des ordinateurs sont mises à rude épreuve pour calculer l’ensemble de Mandelbrot en temps réel.
Certains se souviendront des heures de calcul nécessaires sur les premiers micro-ordinateurs pour obtenir de spectaculaires représentations de l’ensemble de Mandelbrot. Aujourd’hui l’ensemble de Mandelbrot sert de test pour les performances des ordinateurs, notamment pour les tests des processeurs parallèles.
Né à Varsovie en Pologne en 1924, Benoît Mandelbrot émigre en France en 1936. Il s’est retrouvé chargé de cours de mathématiques et membre du séminaire Jean Piaget de 1955 à 1957. Il fut chercheur dans le centre Thomas B. Wason d’IBM dès 1958. Il a été nommé officier de la Légion d’Honneur en 2006.
L’ensemble de Mandelbrot est très simple à décrire : il s’agit de l’ensemble des points du plan complexe pour lesquels la suite :
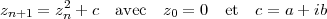
ne diverge pas, ne tend pas vers l’infini.
Pour ceux qui ne se souviennent plus des nombres complexes, ce petit rappel
devrait suffire : un nombre complexe peut s’écrire sous la forme z = x + iy où
i =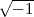 
. On dit que x est la partie réelle et y la partie imaginaire. Lorsque
l’on multiplie z par lui-même ou que l’on élève au carré, on obtient :
z2 = (x + iy)(x + iy) = x2 + 2ixy -y2. Si l’on ne considère que les parties réelles
et entières, on peut donc réécrire :
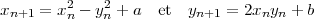
On peut démontrer que dès que le module de zn (on écrit |zn| =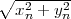 
)
dépasse strictement 2, la suite diverge vers l’infini. Donc c est en dehors de
l’ensemble de Mandelbrot. On arrête donc le calcul dès que le module dépasse 2.
Pour les autres points, ceux de l’ensemble de Mandelbrot, il faut cesser les calculs
à un certain moment puisque la suite ne diverge pas. L’image n’est donc qu’une
approximation du vrai ensemble.
Souvent on affiche des points qui se trouvent en dehors de l’ensemble de Mandelbrot en les coloriant différemment : la couleur dépend du nombre d’itérations avant que la suite ne soit déclarée comme divergente.
En agrandissant des portions de l’image on découvre tout un monde dans lequel le motif initial se retrouve fréquemment. Cette auto-similarité est une des caractéristiques des fractales. La représentation de l’ensemble de Mandelbrot nécessite des calculs importants : si l’on considère les points du plan complexe entre -2 et 0.5 pour la partie réelle et entre -1.25 et 1.25 pour la partie imaginaire, 100 itérations avant de cesser les calculs et une résolution de 500 par 500, il faut près de 2’500’000 calculs.
Le but de l’exercice est de représenter l’ensemble de Mandelbrot avec coloriage et en autorisant les agrandissements de certaines portions de l’ensemble.
Pour simplifier les calculs, il est conseillé de se restreindre aux nombres réels et renoncer aux nombres complexes. C’est possible en se contentant des formules sur les parties imaginaires et réelles.
Souvent le domaine pris en considération pour l’ensemble de Mandelbrot est le plan complexe avec c = a + ib, -2 ≤ a ≤ 0.5 et -1.25 ≤ b ≤ 1.25. La résolution est choisie en fonction des performances de l’ordinateur utilisé. Le seuil à partir duquel on cesse les calculs est souvent fixé à 30. Pour obtenir une image plus fine et plus précise, on augmente le seuil. La performance s’en ressent rapidement.
Pour colorier l’ensemble de Mandelbrot, on peut prendre une palette de couleurs en jouant sur les niveaux ou une palette aléatoire : chaque niveau entre 1 et le seuil est interprété par une couleur différente.
La solution actuellement proposée est donnée en Java : Mandelbrot.java, MandelbrotPanel.java et MandelbrotApplet.java. L’applet compilée peut être testée ci-dessous :