Chapitre 105
Vie, mort et résurrection

Résumé : Le jeu de la vie n’est pas à proprement parler un jeu mais un automate cellulaire. Sur une grille à deux dimensions, théoriquement infinie, il y a des cellules vivantes ou mortes. L’évolution d’une cellule est déterminée par les voisins au nombre de huit. Une certaine analogie avec la vie peut être perçue : les cellules peuvent naître, mourir ou renaître. Ce modèle extrêmement simple a donné lieu à des motifs complexes : puffeurs, canons, oscillateurs, vaisseaux, etc.

Mots-clés : simulation, modèle, automate.

Enoncé

L’exercice s’inspire de la description d’un automate cellulaire imaginé par John Horton Conway, professeur de mathématiques à Cambridge, en 1970.

L’automate cellulaire qui porte le nom de jeu de la vie est en réalité basé sur des règles très simples : l’évolution des cellules est déterminée par l’état de ses huit voisines :

• une cellule morte possédant exactement trois voisines vivantes, naît ;
• une cellule vivante possédant deux ou trois voisines vivantes, survit ;
• sinon elle meurt.

On a pu trouver des analogies entre le jeu de la vie et le développement, le déclin et les changements de colonies de cellules.

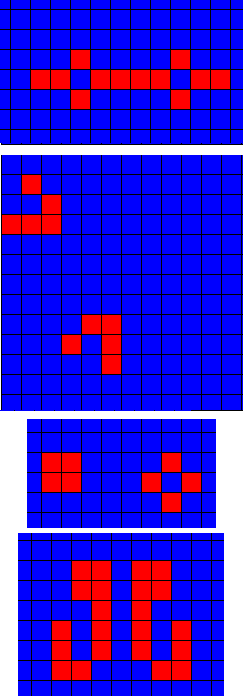
Rapidement, on peut constater que certaines configurations de cellules sont stables voire, périodiques. Plusieurs structures furent découvertes dans le cas où la population de cellules n’explosait pas :

• les oscillateurs sont des structures qui se transforment de manière cyclique ;
• les navires spaciaux sont des structures capables de se déplacer après plusieurs générations ;
• les générateurs de fumée ou puffeurs sont des structures qui laissent des traces derrière elles ;
• les canons, lanceurs ou lance-navires sont capables de produire des vaisseaux à un certain rythme :
• les extenseurs, les chasse-neige, les stores vénitiens, les dents de scie, etc.

Les méthodes utilisées pour obtenir de nouvelles structures font appel à la programmation. On ne peut pas se contenter d’essayer des configurations au hasard. En général, on perfectionne des solutions connues en les recomposant différemment.

Le but de l’exercice est de permettre d’observer le comportement du jeu de la vie en choisissant ses propres structures.

Indications

La programmation du jeu de la vie est assez simple. On peut se contenter d’une matrice ou tableau à deux dimensions dont la taille peut être paramétrée. Chaque case contient la valeur 1 si la cellule est vivante, 0 si elle est morte. Pour la configuration initiale, il est souhaitable de pouvoir saisir des structures connues en cliquant sur des cases du tableau ou alors, choisir des cases au hasard et observer le comportement.

Pour produire la génération suivante, il faut appliquer les règles mentionnées plus haut. Il faut toujours faire attention de ne pas modifier les valeurs du tableau avant d’avoir terminé les calculs. Sinon le statut des cellules pourrait être modifié avant d’avoir fait les calculs sur toutes les cellules.

Les dimensions de la grille ne peuvent pas être infinies dans une simulation informatique. Certaines variantes du jeu de la vie considèrent que le jeu se déroule sur un tore : la case au-dessus de la dernière cellule en hauteur est celle du bas de l’écran, etc.

Des informations complémentaires peuvent être obtenues sur le site : http://t0m.free.fr/jdlv/jdlv_vivant.htm. L’article intitulé « Le Jeu de la vie, toujours vivant... », écrit par Jean-Paul Delahaye donne de nombreuses explications complémentaires et des exemples de figures stables et périodiques.

Solutions

La solution actuellement proposée est donnée en Java : JeuDeLaVie.java et JeuDeLaVieApplet.java. L’applet compilée peut être testée ci-dessous :