Résumé : musique et informatique, c’est possible d’en faire aujourd’hui. Mais, comme pour toute chose, il est intéressant de commencer par le début : expliquer à son ordinateur la gamme. Evidemment, il faut encore savoir laquelle. Au travers d’un bref historique, cet exercice permettra de reconstituer la gamme et de jouer quelques notes.
Mots-clés : musique, gamme, note, fréquence, rapport, consonance, son.
Dans ses dialogues à la fois drôles et intelligents, Ian Stewart donne ses visions des mathématiques chaque mois dans Pour la science. Pour expliquer la gamme musicale à ses interlocuteurs imaginaires, il décide de raconter les relations entre la musique et les mathématiques (No 151, mai 1990). Pour ceux qui aiment ce sujet, Musique, nombres et ordinateurs est un article sur ce sujet paru dans La recherche, No 278, juillet-août 1995, Vol. 26.
« La musique occidentale actuelle est fondée sur une échelle de notes que l’on nomme do, ré, mi, fa, sol, la, si, et sur deux signes : ♯ (dièse) et ♭ (bémol). A partir de do, par exemple, les notes successives sont : do, do dièse ou ré bémol, mi, fa, fa dièse ou sol bémol, sol, sol dièse ou la bémol, la, la dièse ou si bémol, si.
» Puis on recommence avec un nouveau do, mais une octave au-dessus du premier. Sur un piano, les notes blanches sont ainsi do, ré, mi, fa, sol, la, si, do ; les notes noires correspondent aux dièses et aux bémols. Le système est étrange : certaines notes, comme do dièse et ré bémol semblent avoir deux noms. Naturellement il existe une explication à ces mystères.
» Le système actuel est le résultat d’une longue évolution ; c’est un compromis qui s’est finalement établi après une histoire qui a commencé avec les Pythagoriciens, en Grèce antique.
» Claude Ptolémée, qui vécut environ 150 ans après J.-C., à Alexandrie, est surtout connu pour son système cosmologique, mais il fut aussi l’auteur d’un traité des Harmoniques, où il présente le système pythagoricien selon lequel les notes doivent être représentées par des rapports de nombres entiers ; ces derniers apparaissent expérimentalement quand on considère un instrument rudimentaire nommé monocorde, sorte de guitare à une corde.
» Les rapports de nombres entiers apparaissent très naturellement quand on pince simultanément deux monocordes, l’un qui émet une note de base, pour une longueur donnée de corde, et l’autre avec une longueur de corde différente : certaines longueurs produisent des notes qui s’accordent mieux à la note de base. Le plus fondamental de ces intervalles est l’octave ; sur un monocorde, l’octave est l’intervalle entre une note formée par une corde à vide et la note du monocorde avec une corde deux fois plus courte. Le rapport des longueurs des cordes qui donnent cet accord harmonieux est égale à 2/1, quelle que soit la longueur de la corde intiale. D’autres rapports correspondent également à des accords harmonieux ; les principaux sont la quarte, associée au rapport 4/3, la quinte, associée au rapport 3/2. Si la corde à vide joue un do, la quarte dont la première note est un do est un fa, trois notes notes plus loin dans la gamme ; de même, la note à la quinte est le sol, quatre notes après le do.
» Pour créer une échelle harmonieuse, les Pythogoriciens cherchèrent les notes obtenues par quintes successives ; les rapports correspondants sont : 1 ; (3/2) ; (3,2)2 ; 3∕2)3 ; (3∕2)4 ; (3∕2)5, soit 1 ; 3/2 ; 9/4 ; 27/8 ; 243/128.
» Sur un piano, ces rapports correspondent approximativement aux notes do, ré, mi, sol, la, si : où est le fa ? L’intervalle entre 81/64 et 3/2 semble plus « grand » que les autres, mais nous pouvons y remédier en ajoutant une quarte, associée au rapport 4/3. Pourquoi 4/3 ? Parce que si nous étions descendus d’une quinte (rapport 2/3), puis remontés d’une octave (rapport 2/1), nous aurions précisément obtenu ce rapport (2 × 2∕3).
» L’échelle, ou gamme, formée correspond approximativement aux notes blanches du piano. Les intervalles entre les notes successives sont de deux type : 9/8 (un ton) et 256/243 (un demi-ton).
» Voici où s’introduisent les notes noires du piano, correspondant aux dièses et aux bémols : un intervalle de deux demi-tons est associé à un rapport de (256∕243)2, soit un rapport 65536∕59049, proche de 1,11. Or un ton est égal à 9/8, soit 1,125 : c’est presque la même chose ! Cette observation fait considérer que l’échelle comporte des irrégularités, auxquelles on remédie en divisant l’intervalle d’un ton en deux parties, chacune étant aussi proche que possible d’un demi-ton.
» Ces divisions peuvent s’effectuer de différentes façons. Celle qui conduit à la gamme chromatique part des rapports (3∕2)n, pour n = -6,-5…5,6. On les ramène à une même octave par des multiplications ou des divisions par 2, et on les classe par ordre croissant. Chaque dièse et la note inférieure forment un intervalle de 2187/2048, soit environ 1,0679 ; chaque bémol et la note immédiatemment supérieure forment un intervalle de 2048/2187 (0.93664). Au centre, la méthode donne des résultats étranges : deux notes fa dièse et sol bémol devraient occuper la même place, mais diffèrent légèrement. D’autres méthodes produisent d’autres distinctions entre les dièses et les bémols, mais, dans tous les cas, on obtient une gamme à 12 notes, très proche de celle des notes noires et blanches du piano.
» Une corde qui vibre est comme une onde stationnaire, et comme il y a un nombre entier de demi-longueurs d’ondes entre les extrémités, on peut faire apparaître les rapports de nombres entiers des Pythagoriciens. Quand on joue une note sur une guitare, il n’y a pas qu’une note sur la corde ; il existe aussi les harmoniques, avec deux ventres, trois ventres, quatre ventres, etc. Ils s’ajoutent pour donner au son sa richesse sonore. Quand on joue deux notes de longueurs d’ondes voisines, des battements apparaissent : l’intensité du son semble augmenter, puis diminuer alternativement de façon assez désagréable. Le même phénomène a lieu quand il existe des battements entre les harmoniques. La façon la plus simple de l’éviter consiste à utiliser les notes dont les longueurs d’ondes sont dans un rapport simple, comme 3/2 ou 4/3, par exemple. Voilà d’où viennent les rapports pythagoriciens.
» Cette théorie fut testée expérimentalement par Hermann von Helmholtz en 1877. Il étudia les battements entres les harmoniques et parvint à prévoir le degré de dissonance entre deux notes à partir du rapport de leurs longueurs d’ondes. Sa théorie décrit très bien les réactions d’auditeurs.
» Il ne peut exister d’échelle « parfaite » à 12 notes fondées sur les rapports pythagoriciens 3/2 et 4/3. Par échelle parfaite, il faut entendre une gamme où les rapports de notes à la note de base sont 1,r,r2,…r12 avec r12 = 2.
» Les rapports pythagoriciens n’ont que 2 et 3 comme facteurs premiers : tout rapport s’exprime sous la forme 2a3b, où a et b sont des nombres entiers positifs ou négatifs. Par exemple, 243/128 est égal à 2-735. Supposons ainsi que le nombre r soit égal à 2a3b, avec r12 = 2 ; alors 212a312b doit être égal à 2, et 212a-1 doit être égal à 3-12b, ce qui est impossible, car la décomposition d’un nombre en facteurs premiers (en l’occurrence 2 et 3) est unique.
» Aucune gamme ne satisfait exactement les conditions pythagoriciennes
d’harmonie. Il serait erroné d’en conclure qu’aucun nombre r ne peut
engendrer une gamme de 12 notes ; l’équation r12 = 2 a une solution
r =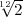 
= 1,059463494…
» La gamme qui est fondée sur nombre est la gamme tempérée, qui présente
bien des avantages. Par exemple, les changements de clé en cours de
morceau sont possibles, alors que les difficultés apparaissent avec la gamme
pythagoricienne : dans cette dernière gamme, si le musicien prend, en
cours de morceau, une autre note que le do de la gamme initiale comme
note de base d’une nouvelle gamme, les notes de la nouvelle gamme ne
correspondent plus aux notes de la gamme initiale. Avec une gamme
tempérée, ce défaut n’apparaît pas et des génies comme Bach peuvent
librement s’exprimer. La gamme tempérée est donc particulièrement utile
si vous voulez jouer d’un même instrument dans différentes tonalités.
Les instruments de musique ne jouant que des notes fixées, comme les
pianos ou les guitares, utilisent généralement la gamme tempérée. Le
demi-ton pythagoricien est égal à 256/243 ou 1,05349 ce qui est voisin de
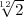; aussi nomme-t-on demi-ton l’intervalle élémentaire de la gamme
tempérée.
En guise d’exercice, il serait intéressant de comparer les gammes (on ajoutera pour l’occasion, celle de Zarlino) :
On peut prendre pour le do, la fréquences fdo = 261.62558Hz.
Nous percevons un son lorsque l’air ambiant ébranle nos tympans. Les sons qui sont généralement considérés comme plaisants peuvent être décrits à l’aide de fonctions périodiques. Si on veut une fonction présentant f oscillations par seconde, il faut écrire y = sin(2πft). Lorsqu’une corde ébranle l’air ambiant en vibrant à la fréquence f, l’amplitude de la vibration y en un point de la corde peut être décrite à l’aide de la fonction y = sin(2πft). Le logiciel MatLab est capable d’enregistrer 8192 fois par seconde l’amplitude d’une telle fonction, de la convertir en tension et de soumettre le haut-parleur à cette tension. Cette technique, qui permet d’obtenir une suite de nombres à partir d’une fonction, est appelée échantillonage.
En MatLab, la commande permettant d’envoyer les amplitudes au haut-parleur est sound(y).
Les solutions sont en cours de développement... Toute solution est la bienvenue.