Résumé : Aristote, le plus grand de tous les philosophes, méritait bien qu’on le commente, ce que fit Averoes (parmi bien d’autres) au XIIe siècle. Saint Thomas d’Aquin commenta ce commentaire (qu’il désapprouvait) et il fut lui-même commenté par Etienne Gilson qui lui-même... Que dire alors du commentaire mathématique ? On peut aborder cette question par un casse-tête, puis on peut prolonger la réflexion sur les structures mathématiques.
Mots-clés : théorie des nombres, langage, évolution, cycle, suite.
Dans son excellent livre, Le Jour des fourmis, Bernard Werber (Albin Michel, 1992) donne un problème (il s’agit d’un concours télévisé) :
« Le visage troublé de Mme Ramirez apparut sur l’écran. Depuis qu’elle pataugeait sur cette nouvelle énigme, cette suite chiffrée, le taux d’audience de l’émission avait doublé. Plaisir sadique de voir quelqu’un jusque-là infaillible soudain chanceler ? Ou bien était-ce parce que le public, s’identifiant plus facilement à eux, préfère souvent les perdants aux gagnants ?
« Avec sa bonne humeur habituelle, l’animateur interrogeait :
— Alors, Madame Ramirez, cette solution, vous l’avez trouvée ?
— Non. Toujours pas.
— Concentrez-vous, voyons, Madame Ramirez ! A quoi vous fait penser notre suite de chiffres ?
La caméra se braqua d’abord sur le tableau puis sur Mme Ramirez qui expliquait, songeuse :
— Plus j’observe cette suite, plus je suis troublée. C’est fort, très fort. Il m’avait semblé quand même repérer quelques rythmes... Le « un », toujours placé à la fin... Des paquets de « deux » au milieu...
Elle s’approcha du tableau où étaient inscrits les chiffres et commenta, à la manière d’une maîtresse d’école :
— On pourrait croire à une progression exponentielle. Ce n’en est pas vraiment une. J’ai cru à un ordre entre les « un » et les « deux » et voilà ce chiffre « trois » qui surgit et se répand lui aussi... J’ai pensé alors que, peut-être, il n’y avait pas d’ordre du tout. Nous avons affaire à un monde de chaos, avec des chiffres disposés de manière aléatoire. Pourtant, mon instinct de femme me souffle qu’il n’en est rien, qu’ils n’ont pas été placés au hasard.
— Et donc, à quoi ce tableau vous fait-il penser, Madame Ramirez ?
La physionomie de Mme Ramirez s’éclaire.
— Je vais vous faire rire, dit-elle.
La salle éclata en applaudissements.
— Laissez réfléchir Mme Ramirez, intervint l’animateur. Elle pense à quelque chose. Et à quoi, madame Ramirez ?
(...)
— Alors, Madame Ramirez, réponse ou joker ?
— Joker. J’ai besoin d’un supplément d’information.
— Tableau ! réclama l’animateur.
Il nota l’empilement connu :

Puis, toujours sans regarder son papier, il ajouta :
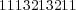
— Je rappelle les phrases-clés. La première était : « Plus on est intelligent, moins on a de chance de trouver. » La deuxième était : « Il faut désapprendre ce que l’on sait. » J’en livre une troisième à votre sagacité : « Comme l’univers, cette énigme prend sa source dans la simplicité absolue. »
Applaudissements. »
Pour ceux qui désirent chercher la solution au problème et aider Madame Ramirez, l’énoncé s’arrête ici.
Pour les autres, l’explication est toute simple (on peut lire également Jean-Paul Delahaye dans Pour la Science, No 219 de janvier 1996), il s’agit d’un commentaire mathématique : prenez un mathématicien (au coeur le plus sec possible) ; donnez-lui le texte numérique le plus élémentaire qui soit : « 1 » ; et demandez-lui son commentaire. Laconique, il répondra : « un ”1” » (signifiant : le texte est composé d’un « 1 »), ce qu’il écrira « 1 1 ». Demandez-lui de commenter ce commentaire numérique. Avec une remarquable efficacité et sans ostentation, il vous dira « deux ”1” ». Continuez ainsi, vous obtiendrez de lui le commentaire « 1 2 1 1 », puis « 1 1 1 2 2 1 », et ainsi de suite...
Facile à dire, mais quelle est cette suite ? Elle aurait été décrite la première fois par l’Allemand M. Hilgemeir dans un article où il démontrait quelques propriétés élémentaires. Il revient cependant à John Conway – célèbre pour son invention du jeu de la vie – d’avoir traité presque toutes les questions posées par ce jeu des commentaires numériques infinis. Ce qu’il a trouvé est étrange, complexe et fascinant.
Pour présenter ses résultats, J. Conway propose d’utiliser le langage de la chimie, de la physique et de la cosmologie. Il imagine un monde qui, seconde après seconde, n’est que le développement des commentaires successifs du texte « 1 ». L’analogie avec le monde physique proposée par J. Conway est la suivante : l’univers engendré par les commentaires numériques sur l’UN se décompose en éléments stables et en éléments instables, et il y a 92 éléments que J. Conway a baptisés du nom des 92 premiers éléments chimiques de Mendeleïev. Les transformations des éléments numériques correspondent, sans être exactement les mêmes, aux transmutations spontanées des éléments physiques.
Pour définir un élément, on considérera que certains nombres N sont une concaténation de deux morceaux G.D qui, dans la suite des commentaires numériques, n’interféreront plus jamais entre eux. G.D est une décomposition du nombre N si, pour tout entier n, nième commentaire de N est obtenu en juxtaposant le nième commentaire de G et le nième commentaire de D. Le nombre 1113213211, par exemple, se décompose en G = 11132 et D = 13211. En effet, les commentaires successifs de 11132 se termineront tous par 2, alors qu’aucun commentaire de 13211 ne commencera par 2 car 13211 → 11131221 → 3113112211 → 132113212221 dont le début est 13211, et donc les premières décimales recommencent de manière cyclique.
Les nombres qui ne peuvent pas être décomposés sont appelés les éléments, ou atomes. Il faut faire attention, ce n’est pas parce qu’un élément apparaît dans un nombre que le nombre se décompose exactement à cet endroit, car il faut que les découpes soient bonnes.
Le résultat suivant, obtenu par J. Conway, indique tous les endroits où l’on peut faire de telles coupures :
« Si le nombre a se termine par un 2 et que b commence par 121, 123, 131, 132, 111, 312, 313, 321, 323, 3112, 3221 ou 3223, alors le nombre ab peut être coupé en a et b.
« Si le nombre a se termine par un 1 ou un 3 et que b commence par 22121, 22123, 22131, 22132, 22111, 22312, 22321, 22323, 223112, 223113, 223221 ou 223223, alors le nombre ab peut être coupé en a et b.
« Les nombres qui ne peuvent pas être coupés s’appellent les éléments. »
L’évolution de l’Univers à partir d’un certain moment n’est donc que la transformation des éléments stables les uns en les autres, selon des règles immuables données dans le tableau ci-dessous. Une sorte de bouillonnement complexe, mais parfaitement réglé, détermine l’avenir des commentaires infinis sur l’UN.
On demande donc de reproduire le commentaire infini sur l’UN, de construire un tableau des transmutations et des éléments et enfin, d’observer la taille de l’Univers : comment croît-elle ? Quels sont les éléments les plus fréquents ? Que se passe-t-il lorsqu’on part d’un élément différent de 1 ? Existe-t-il des suites numériques infinies qui, lorsqu’on en fait le commentaire, soient égales à elles-mêmes ? Une telle suite serait son propre commentaire, comme, dans le cas fini, le nombre 22 est son propre commentaire (22 est la seule suite finie qui soit égale à son commentaire). Considérez également le commentaire suivant : on part d’une suite de nombres, par exemple, (9 3 1 2 1 9), en comptant le nombre de « 0 » s’il y en a, puis le nombre de « 1 », etc., et écrivons dans cet ordre les résultats. Ici on obtient (2 1 1 3 2 9), etc.
Il est conseillé d’adopter un algorithme simulant le commentaire : on parcourt la liste en comptant le nombre d’éléments identiques ; on les note, et on poursuit cette opération jusqu’à ce que la chaîne soit complètement parcourue. On recommence cette opération sur la nouvelle chaîne.
Le tableau des transmutations permettra de proposer plus facilement un tableau d’expansion de l’Univers.
La solution actuellement proposée est donnée par les fichiers MatLab : commentaire.m
Une autre solution est également proposée en Mathematica par F. Haeberli et B. Vuilleumier : suitecom