Résumé : le jeu de Marienbad ou Fan-Tan ou jeu de Nim est très répandu et très simple. Il se joue à deux joueurs ; chacun à son tour enlève d’un tas un certain nombre de jetons ; celui qui enlève le dernier a perdu. Ce jeu admet une théorie mathématique des plus inattendues, basée sur la numération binaire.
Mots-clés : numération binaire, graphe.
Dans le film d’A. Resnais Année dernière à Marienbad, on voit M, au fil d’énigmatiques déambulations dans un château, proposer à ses interlocuteurs de jouer avec lui à un jeu de société. Il dispose quelques jetons sur une table. La règle est simple et aucune habileté ne semble nécessaire pour triompher. Mais voilà. La partie tourne systématiquement à l’avantage de M. « JE PUIS PERDRE, MAIS JE GAGNE TOUJOURS... » assure-t-il à son protagoniste inexorablement vaincu...
Troublante sentence dont la portée symbolique n’aura nullement échappé aux nombreux cinéphiles qui ont vu et revu ce beau film. Mais tout cela tient simplement à quelques propriétés mathématiques du jeu lui-même.
On dispose sur une table de quatre rangées de jetons : la première en comporte 7, la deuxième 5, la troisième 3 et la quatrième 1.
Il y a deux joueurs A et B. Chacun joue à son tour et enlève le nombre de jetons qu’il veut dans une seule rangée à la fois. Celui qui enlève le dernier a perdu. Il peut enlever toute une rangée s’il le désire mais n’a pas le droit de passer son tour.
A joue le premier et... perd. Ce résultat n’est nullement dû à l’inexpérience de A, encore moins au hasard. A perd PARCE QU’IL JOUE EN PREMIER et surtout parce que B applique une stratégie qui lui assure la victoire QUOI QUE FASSE A. Tout cela tient du paradoxe car, à première vue, A jouant le premier, celui-ci possède plus de possibilités que B... il pourrait être sur l’offensive alors que, de fait, il est sur la défensive. La théorie des graphes arrive à point nommé pour le faire comprendre.
Ce problème est tiré de la Grande encyclopédie alpha des sciences et techniques, Editions Atlas, Paris, 1976.
La réalisation informatique doit permettre à un joueur de jouer contre l’ordinateur en faisant en sorte que celui-ci applique la stratégie gagnante décrite plus haut.
On associe au jeu de Marienbad un graphe, c’est-à-dire un ensemble de sommets et de flèches qui représentent toutes les possibilités ainsi que les coups permis. Le schéma ci-dessous donne un exemple de partie.
Pour comprendre l’utilité d’un graphe, on peut se restreindre à la
fin de la partie. Si on part de la position 
, le joueur B doit choisir
un sommet du graphe relié à celle-ci par une flèche. En l’occurrence il
choisit 
, le joueur A procède de façon semblable et choisit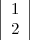 
. Il ne
reste plus qu’à se placer en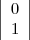 
pour faire mordre la poussière à son
adversaire.
Le problème est donc ramené à : déterminer le noyau du graphe qui contient
les positions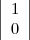 
et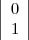 
; il s’agit donc de trouver une succession de sommets S
qui possède la propriété suivante : si, au cours du jeu, un des joueurs parvient une
fois à choisir un sommet de S, il pourra toujours lors des coups suivants choisir un
sommet de S et ceci jusqu’aux positions 
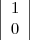et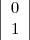 
qui lui assurent la
victoire. De plus la structure de S est telle que son adversaire ne peut
dès lors absolument pas en faire autant : car l’on peut ‘sortir’ de S, y
‘entrer’ (toujours), mais on ne peut pas y rester pendant deux coups
consécutifs. Les joueurs jouant chacun à leur tour, celui qui parvient une fois à
rentrer dans S est sûr de pouvoir y retourner à chaque fois qu’il joue et
d’obliger ainsi son adversaire à rester en dehors jusqu’à la fin où celui-ci
est forcé de prendre la position 
, c’est-à-dire d’enlever le dernier
jeton.
Pour déterminer le noyau S, il est conseillé d’utiliser une méthode numérique (fondée sur certains concepts de la théorie des graphes, fonctions de Grundy) faisant appel à la numération binaire. Après avoir converti les nombres de jetons de chaque rangée en base 2, il suffit de les additionner (en jetant les restes). On observe sur le schéma de la partie donnée en exemple que cette somme notée Σ vaut zéro lorsque la position appartient à S. Il faut donc ôter le nombre de jetons nécessaires pour conserver cette somme à 0, sauf en fin de partie.
Les solutions sont en cours de développement... Toute solution est la bienvenue.