Résumé : combien de parts peut-on obtenir en découpant un cercle par n droites ? Combien de points d’intersection peut-obtenir au maximum ?
Mots-clés : théorie des graphes, combinatoire, formule d’Euler, triangle de Pascal.
Combien de morceaux de pizza peut-on obtenir en la découpant à l’aide de n coups de couteau. Ou encore, quel est le nombre maximal Ln de régions définies par n droites dans le plan. Ce problème a été résolu pour la première fois en 1826 par le mathématicien suisse Jacob Steiner.
On peut formuler ce problème encore différemment. Sur un cercle, on marque n points de telle façon que, lorsque l’on trace toutes les cordes possibles les unissant deux à deux, il n’y ait pas trois cordes concourantes. Combien y a-t-il de points d’intersection à l’intérieur du cercle. En combien de régions le disque se trouve-t-il divisé par ces cordes ?
Peut-on parcourir sans lever le crayon du papier et sans passer deux fois par le même segment tous les arcs et cordes représentés sur le disque ? Ou encore, le graphe déterminé par les n points, les cordes les unissant et les arcs entre deux points contigus des n donnés, est-il eulérien ?
Cet exercice est tiré du livre Aventures mathématiques de Miguel de Guzmán publié aux Presses polytechniques et universitaires romandes, 1990 et de Concrete Mathematics de Graham, Knuth et Patashnik publié chez Addison Wesley, 1989.
Il est conseillé de commencer par observer des cas simples. Un plan avec aucune droite possède une seule région, avec une droite, on a deux régions et avec 2 droites on a quatre régions. On peut alors construire un tableau dont la première colonne indique le nombre de points sur le cercle, la deuxième, le nombre de droites (ou coups de couteau), la troisième, le nombre de points d’intersection et la quatrième, le nombre de régions.
Après ces premières observations, on peut tenter la généralisation. Pour démontrer la formule, la méthode par induction est recommandée.
Pour le nombre de points d’intersection (ou points intérieurs), il est conseillé de comparer les résultats réunis dans le tableau avec le triangle de Pascal.
Pour déterminer le nombre de régions on peut essayer de trouver une relation de récurrence et déterminer Ln en fonction de Ln-1. Pour évaluer Ln on peut faire appel à la formule que Gauss a découverte en 1786 à l’âge de 9 ans afin de calculer la somme des entiers de 1 à n :
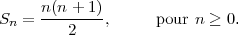 | (3.1) |
Un graphe est un ensemble de sommets et d’arêtes les unissant. Pour prouver que le graphe est eulérien, il suffit de démontrer que le nombre de sommets est de degré impair, c’est-à-dire, le nombre de sommets où concourt un nombre impair d’arêtes est 0 ou 2.
La solution actuellement proposée est donnée par les fichiers MatLab : pizza.m et cercle.m