droitegauchehaut

Chapitre 2
Exemple

Le problème choisi pour servir d’exemple est très simple. Il est tiré d’un excellent livre, Concrete Mathematics de Graham, Knuth et Patashnik publié chez Addison Wesley, 1989. Il s’agit de trouver une formule permettant de calculer à l’aide d’un nombre fini d’opérations élémentaires la somme des carrés des n premiers entiers :

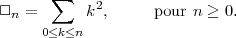
∑ □n = k2, pour n ≥ 0. 0≤k≤n

La formulation peut être également (tirée de Jeux Mathématiques et logiques, La fraction du bicentenaire, Vol.5, Hatier, 1990) : dans un quadrillage 3x3 on peut compter 14 carrés. Mais combien peut-on compter de carrés dans un quadrillage 85x85 ?

Avant d’agir, essayez de comprendre. La notation n’est peut-être pas évidente pour tout le monde. Le problème consiste à calculer la somme des carrés des nombres de 0 à n. Dans le cas où n = 4, alors cette somme vaut : 0 + 1 + 22 + 32 + 42 ou encore, 0 + 1 + 4 + 9 + 16 = 30. La notation choisie pour représenter le problème fait appel au symbole ∑ qui indique la somme ; sous le symbole on indique le domaine sur lequel la somme porte (les nombres entre 0 et n, ou encore : 0 ≤ k ≤ n) ; à droite du symbole de sommation, on indique l’expression impliquée dans la somme (k2 symbolise le nombre k élevé au carré). Cette notation a l’avantage de présenter une expression générale correspondant au problème posé. Choisissez une bonne notation.

Recherchez des stratégies, Cherchez des ressemblances avec d’autres problèmes. Le problème ressemble à un classique, la somme de n premiers entiers. Gauss avait trouvé une méthode séduisante en 1786, il avait 9 ans :

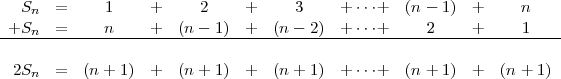
S = 1 + 2 + 3 + ⋅⋅⋅+ (n - 1) + n n -+Sn---=-----n----+---(n---1)-+---(n---2)-+-⋅⋅⋅+-----2-----+-----1----- 2Sn = (n + 1) + (n + 1) + (n+ 1) + ⋅⋅⋅+ (n + 1) + (n + 1)

En simplifiant, on trouve

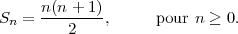
Sn = n-(n-+-1), pour n ≥ 0. 2

Commencez par ce qui est facile. Le plus simple est de commencer par les premières valeurs de n.

Faites des expériences et cherchez des traits communs, des règles. L’expérience se résume au calcul de certaines valeurs :

| --n---0--1--2---3----4---5---6----7-----8----9----10---11----12-- n2 |0 1 4 9 16 25 36 49 64 81 100 121 144 -□---|0--1--5---14--30--55---91--140---204--285--385---506--650-- n |

Faites un schéma. Un programme informatique élémentaire permet de visualiser le comportement de la somme pour les premières valeurs de n.

% Initialisation  
 n=0:12;        % Valeurs de n  
 n2=n.^2;       % Calcul des carrés  
 s=0;  
 r=[];  
 for i=1:length(n)  
   s=s+n2(i);  % Somme des carrés  
   r=[r, s];   % Mémorisation des résultats  
 end  
% Affichage des résultats  
 n  
 n2  
 r  
% Resprésentation graphique  
 plot(n,n2,’-’,n,r,’--’)

Le résultat est affiché dans la figure ci-dessous.

Somme des carr\let \prOteCt \relax \Protect \csname acp:c\endcsname {20}es

Modifiez le problème pour trouver un autre chemin possible. Si l’on considère un terme de plus à la somme, on a alors

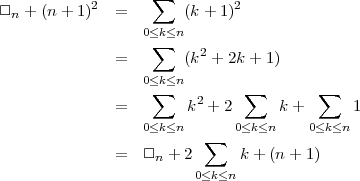
2 ∑ 2 □n + (n + 1) = (k + 1) 0≤k≤n = ∑ (k2 + 2k + 1) 0≤k≤n ∑ ∑ ∑ = k2 + 2 k + 1 0≤k≤n 0≤k≤n 0≤k≤n ∑ = □n + 2 k + (n + 1) 0≤k≤n

Malheureusement, on peut déduire une formule pour la somme des n premiers entiers et non la somme de leurs carrés.

Menez à terme les meilleures idées. Si l’on prend la somme des cubes, trouverait-on une expression pour les carrés ? Il suffit d’essayer. Ne vous découragez pas.

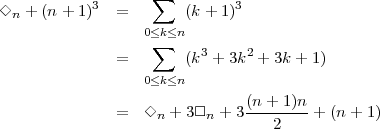
◊ + (n + 1)3 = ∑ (k + 1)3 n 0≤∑k≤n = (k3 + 3k2 + 3k + 1) 0≤k≤n (n + 1)n = ◊n + 3 □n + 3--------+ (n + 1) 2

On fait disparaître ◊n et on obtient

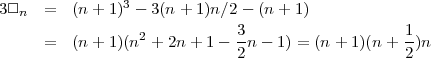
3 3□n = (n + 1) - 3(n + 1)n∕2- (n + 1) = (n + 1)(n2 + 2n + 1- 3n - 1) = (n + 1)(n+ 1)n 2 2

Analysez bien les résultats avant de les admettre. En reprenant le tableau décrit plus haut, on constate que la formule est vérifiée dans ces cas.

Pensez à des techniques générales : récurrence, induction,...

Supposons donc que la formule soit

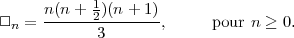n(n + 1)(n + 1) □n = ------2--------, pour n ≥ 0. 3
(2.1)

par induction, si l’on considère

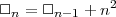
□n = □n -1 + n2

alors, en utilisant la formule (2.1),

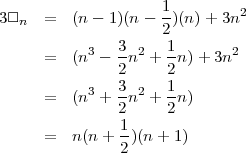
3 □n = (n - 1)(n - 1)(n)+ 3n2 2 = (n3 - 3-n2 + 1n)+ 3n2 2 2 3 3- 2 1- = (n + 2 n + 2n) 1- = n(n+ 2)(n+ 1)

Il y a de quoi être satisfait. Analysez votre propre stratégie. La méthode a permis de résoudre le problème.

Regardez si l’on ne peut pas faire plus simplement. Bien entendu, il y a d’autres méthodes pour résoudre le problème. On peut citer : la recherche de la solution dans la littérature (la recherche d’information est très utile, mais l’approche permet difficilement de se rendre compte de ses capacités à résoudre un problème), le remplacement de la sommation par une intégrale, l’utilisation des développements en série, etc.

Examinez si la méthode peut être utilisée à d’autres fins. La deuxième formulation du problème conduit à l’utilisation du même résultat. Si l’on considère un quadrillage n × n, alors il y a un seul carré de côté n, 4 carrés de côtés (n - 1)… et p2 carrés de côtés n - p + 1. Pour n = 85, on obtient 208 335 carrés.

L’emploi de l’informatique pour résoudre les problèmes permet, en plus des méthodes traditionnelles, l’expérimentation à grande échelle, les représentations graphiques de qualité, la simulation et la modélisation. Les exercices proposés plus loin peuvent être résolus avec ou sans l’aide de l’informatique. L’accès à l’ordinateur et à la programmation permet toutefois à l’élève de se rendre compte aisément et rapidement de la qualité des solutions trouvées. Ainsi les approximations numériques, les interpolations, les résolutions graphiques seront un atout supplémentaire.

droitegauchehaut