Résumé : pour simuler la marche d’un être humain ou d’un animal, on peut utiliser des règles simples. Celles-ci permettent même de déterminer la vitesse potentielle d’animaux disparus. C’est de cette façon que l’on a déterminé à quelle vitesse pouvaient se déplacer, par exemple, des dinosaures.
Mots-clés : simulation, mouvement, accélération, vitesse, gravitation.
Le sujet est inspiré de l’article Walking and running de R. Mc Neill Alexander paru dans The mathematical gazette, volume 80, No 488 de juillet 1996.
Le corps humain est une machine compliquée dont les mouvements impliquent différentes articulations et un grand nombre de muscles. Chaque position du corps humain peut être décrite en donnant les angles aux articulations. Le nombre d’angles nécessaires pour décrire de façon non ambiguë est appelé le degré de liberté. Par exemple, la position du genou est décrite par un seul angle. On dit, alors, qu’il n’a qu’un seul degré de liberté. La cheville, quant à elle, permet des rotations autour de deux axes. A ce moment-là, on dira qu’il y a deux degrés de liberté. Au total, il y a six degrés de liberté dans chaque jambe, ce qui en fait douze et qui nous suggère qu’il faut douze équations pour décrire le mouvement de la marche. Si l’on tenait compte de la flexibilité du pied et des mouvements des bras, on devrait ajouter encore plus d’équations.
Un modèle de la marche identifie vingt-neuf muscles dans chaque jambe, cinquante-huit en tout. On doit également connaître la force que l’on peut exercer sur chaque muscle, mais il est difficile d’évaluer cinquante-huit inconnues en résolvant un ensemble de douze équations simultanées. On considérera donc un modèle beaucoup plus simple et la situation de la marche peut être considérablement simplifiée.
Si l’on observe quelqu’un qui marche et que l’on essaie de découvrir l’essence du mouvement, on constate que le pied se déplace alternativement, chacun étant levé juste après que l’autre soit posé. Lorsqu’un pied est sur le sol, le genou est pratiquement déplié, conservant la distance entre la hanche et la cheville pratiquement constante. Comme conséquence, les corps montent et descendent d’environ à peu près trois centimètres à chaque pas. On est au point le plus élevé lorsque la jambe qui supporte le corps est verticale. Ce mouvement peut être représenté par un modèle très simple (voir figure ci-après).
On doit se rappeler maintenant qu’un corps se déplace le long d’un arc de cercle et on peut considérer son accélération vers le centre du cercle. Cette accélération est donnée par la vitesse au carré divisée par le rayon. Dans le cas de notre promeneur, le rayon est la longueur de la jambe, on va l’appeler L. Ainsi, si la vitesse est v, l’accélération est donnée par v2∕L.
Lorsque le marcheur est à la verticale et sa jambe complètement droite, le promeneur ne peut pas tomber avec une accélération plus grande que l’accélération gravitationnelle g.
Ainsi,
Cette équation nous indique la vitesse maximale possible.
Le problème consiste donc à simuler le déplacement d’un marcheur humain et de déterminer les valeurs possibles de la vitesse en fonction de la longueur des jambes. Pour les êtres humains, il n’y a que deux genres de déplacement : marcher et courir. Pour les chevaux, les chiens et les autres mammifères à quatre pattes, il y a d’autres façons de se déplacer : la marche, le trot, le galop. Est-ce que l’on peut prédire les vitesses auxquelles les différents mammifères doivent changer de façon de se déplacer ? Si un cheval cesse un galop à six mètres par seconde, à quelle vitesse observe-t-on le même comportement chez un chien ? Comme les animaux ne se déplacent pas sur deux jambes, il faut trouver une approche plus générale pour modéliser le déplacement. On considérera le concept de similarité dynamique.
On dit que deux systèmes sont similaires dynamiquement si on peut les
considérer comme identiques en multipliant toutes les longueurs par un seul
facteur. Par exemple, deux pendules de différentes longueurs se déplaçant avec le
même angle ont le déplacement similairement dynamique. Dans quelles
circonstances on peut considérer que des animaux de tailles différentes sont
dynamiquement similaires ? Leurs corps doivent être géométriquement similaires
et ils doivent se déplacer à des vitesses approximatives. Lorsque les animaux
marchent ou courent, ils montent et descendent à chaque pas, gagnant ou perdant
de l’énergie potentielle. Ils accélèrent également ou ralentissent à chaque
pas, gagnant ou perdant de l’énergie cinétique. Il semble clair que la
similarité dynamique est possible seulement si deux animaux ont les mêmes
rapports d’énergies potentielle et cynétique. Si un animal dont le poids est
de masse m tient sur des pattes de longueur L, son énergie potentielle
est mgL. S’il se déplace à la vitesse v, son énergie cynétique est 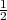 mv2.
Donc,
mv2.
Donc,
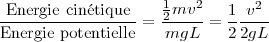
La similarité dynamique n’est possible pour des animaux de différentes tailles seulement si leurs vitesses sont telles que la valeur indiquée ci-dessus est égale (v2∕gL). Cette valeur sans unité est appelée nombre de Froude, d’après l’ingénieur victorien qui a utilisé des nombres semblables dans l’analyse de la résistance aux vagues du déplacement des bateaux, mais c’est une autre histoire.
Pour rejoindre l’équation du mouvement (30.2) de la marche, on peut réécrire cette équation d’une façon différente. On ne peut marcher avec un nombre de Froude plus grand que 1, sinon on court. L’avantage du nombre de Froude est qu’il n’est pas lié à un modèle particulier de marche. Il suggère une hypothèse générale : des animaux de formes semblables et de différentes tailles vont se déplacer dynamiquement de la même façon, lorsque les nombres de Froude sont égaux. Ils feront des changements de déplacement, de la marche au trot ou du trot au galop, à des vitesses pour lesquelles le nombre de Froude sont égaux. Si l’on compare un chien avec un cheval dont les pattes sont quatre fois plus longues, le cheval doit se déplacer à deux fois la vitesse du chien – la racine carrée de quatre – et il doit changer de façon de se déplacer à deux fois la vitesse pour laquelle le chien change également sa façon de se déplacer. De façon générale, les mammifères, depuis les plus petits jusqu’aux girafes, passent de la marche au trot à un nombre de Froude d’environ 0,5 et du trot au galop à un nombre de Froude d’environ 2,5.
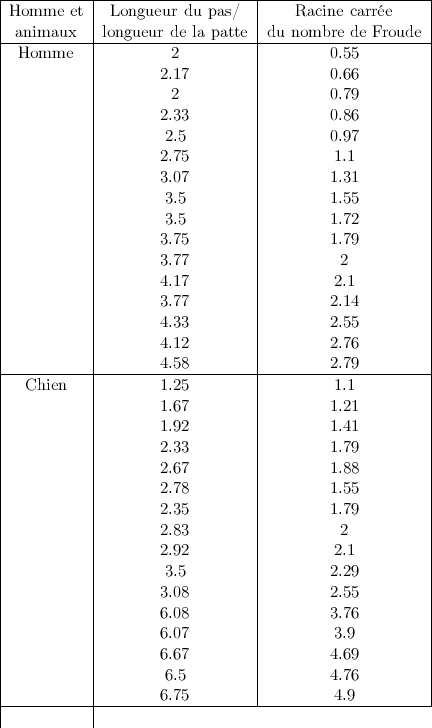
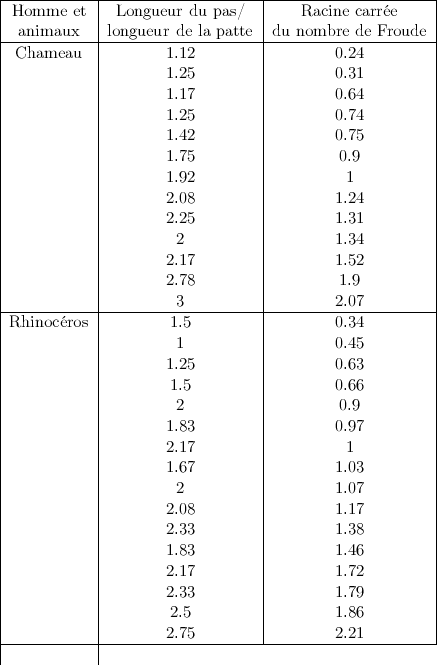
Lorsque l’on observe les traces laissées par les dinosaures dans le sable et qui ont été changées en pierre, on peut mesurer la longueur des pas, c’est-à-dire la distance entre l’emplacement du même pied lors d’un déplacement successif. Avec cette information, on peut estimer la longueur du pas par rapport à la longueur de la jambe. Avec cette information, on peut estimer le nombre de Froude auquel les dinosaures marchent ou courent.
Dans l’exercice, on tiendra compte de certaines valeurs observées, par exemple chez les êtres humains, les kangourous, les chameaux, les chiens, etc. et l’on comparera avec les nombres de Froude des autres animaux disparus, comme les dinosaures pour estimer à quelle vitesse ils se déplaçaient en marchant et à quelle vitesse ils pouvaient courir.
On peut également transposer ce comportement aux déplacements sur la lune. Si, en effet, on considère que l’accélération de la gravitation n’est plus de 10m∕sec2, mais 1,6m∕sec2, on peut déterminer la vitesse maximale pour marcher sur la lune et à partir de quelle vitesse on devrait courir. C’est certainement l’explication pour laquelle les astronautes ne marchaient pas sur la lune , mais sautaient, sinon ils auraient dû se déplacer de façon intolérablement trop lente.
Pour résoudre ce problème, il est conseillé de représenter graphiquement la marche d’un être humain, de tenir compte éventuellement du déplacement lors de la course, de déterminer des tables en fonction des longueurs des jambes et déterminer ainsi les vitesses maximales, de comparer les vitesses de déplacement d’un enfant à celui d’un adulte ou bien d’un adulte sur la terre par rapport à un adulte sur la lune. Pour les nombres de Froude on considérera la table donnée ci-après qui, en interpolant, permettra de déterminer les vitesses de déplacement de différents animaux, voire de certains animaux disparus.
Les solutions sont en cours de développement... Toute solution est la bienvenue.