Chapitre 29
Le problème du radar

Résumé : lorsqu’un avion survole un lieu et qu’il est repéré par un radar, comment l’indiquer à un deuxième radar ?

Mots-clés : coordonnée sphérique, coordonnée géocentrique, coordonnée géographique, géoïde, ellipsoïde, rotation, changement de repère.

Enoncé

Un système de contrôle par radars dans le contrôle du trafic aérien reçoit différentes informations de radars situés à différents endroits du globe. Cette information contient, entre autres, les coordonnées x,y,z (selon le système de coordonnées du radar qui émet l’information) d’un avion ”vu” par le radar.

Le problème peut être résumé comme suit : soit deux radars R₁ et R₂ situés aux points P₁ et P₂ du globe. Un avion A est ”vu” par le radar R₁ dans son système local en coordonnées cartésiennes avec comme coordonnées (x₁;y₁;z₁). Il est demandé de déterminer les coordonnées (x₂;y₂;z₂) de l’avion dans le système de coordonnées cartésiennes du radar R₂. Les points P₁ et P₂ sont donnés par les coordonnées géographiques (en degrés, minutes et secondes) (f₁;l₁) et (f₂;l₂), où f₁,f₂ sont les latitudes et l₁,l₂ les longitudes.

Pour résoudre ce problème, il faut résoudre quelques problèmes annexes : la conversion de degrés (minutes, secondes) en radians et la transformation de coordonnées géographiques en coordonnées géocentriques. Il est important, en effet, de se souvenir que les coordonnées géographiques ne sont pas des coordonnées sphériques : la latitude géographique est déterminée en mesurant l’angle d’un objet (soleil, lune, étoile) dans le ciel au-dessus de l’horizon, ou encore, l’angle entre un plan tangent à la surface du globe et l’objet.

Ce problème est tiré de Solving Problems in Scientific Computing Using Maple and Matlab de Walter Gander et Jiří Hřebíček chez Springer-Verlag, Berlin, 1993.

Indications

Pour la transformation des coordonnées géographiques (f,l) d’un point P en coordonnées géocentriques cartésiennes (x_c,y_c,z_c), on considère C, le centre de la terre, l’axe z_c, l’axe passant par les pôles terrestres avec orientation positive vers le pôle nord, l’axe x_c, l’axe passant par le méridien zéro et le 180e avec orientation positive vers le méridien de Greeenwich et l’axe y_c, l’axe perpendiculaire aux axes x_c et z_c avec orientation positive vers le 90e méridien.

La forme le la terre est un géoïde mais, pour ce problème, on utilisera une approximation décrite par un ellipsoïde circulaire. Les axes de révolution des deux corps sont les mêmes. La section d’un ellipsoïde est une ellipse (de KRASOVSKY), avec le demi grand axe A = 6378.245[km] et le demi petit axe B = 6356.863[km]. Pour obtenir les équations de la transformation, il est utile de passer à la représentation paramétrique d’une ellipse :

Pour relier l’angle f à x et z, il suffit de calculer le vecteur normal 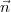à (x;z) et d’en déduire une expression pour tan(φ), puis cos(φ) et sin(φ).

Pour résoudre le problème du radar, il suffit de passer du système de coordonnées pour lequel l’avion a été repéré (premier radar P₁ = (f₁;l₁)) dans le système de coordonnées du deuxième radar P₁ = (f₁;l₁). Pour effectuer cette transformation, il faut procéder successivement à une translation et à trois rotations :

• la translation consiste à placer le système de coordonnées situé à l’intersection de l’équateur et du méridien de Greenwich au point P₁ : il faut donc modifier d’abord l’orientation des axes (l’axe z devient axe des x (avec orientation négative vers C), l’axe x devient l’axe des y et l’axe y devient l’axe des z) ; puis on fait subir une rotation autour du nouvel axe des y d’un angle l₁ et enfin, une rotation autour du nouvel axe x une rotation d’un angle f₁. Les coordonnées de l’avion se calculent alors en prenant les anciennes coordonnées moins le vecteur distance _P (P₁) entre les deux radars (exprimée dans ce nouveau système de coordonnées) ;
• la première rotation consiste à tourner le système de coordonnées autour de l’axe des x d’un angle f₁ afin de placer l’axe des y parallèle à l’axe des z_c de la terre ;
• la deuxième rotation consiste à tourner le nouveau système de coordonnées autour de l’axe des y d’un angle Δl = l₂ -l₁ afin de faire coïncider les axes des x ;
• la troisième rotation consiste à faire tourner le système de coordonnées ainsi obtenu autour de l’axe des x d’un angle f₂ pour faire coïncider le système avec P₂.

En résumé, les coordonnées de l’avion exprimées du point de vue du deuxième radar s’obtiennent en combinant les transformations suivantes :

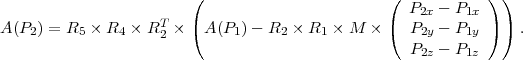
A titre d’exemple, on pourra prendre les coordonnées respectives des radars situés à Genève Cointrin et à Zurich (données aimablement fournies par l’aéroport de Genève Cointrin) : P₁ = (46^∘14′23′′;6^∘6′37′′), P₂ = (47^∘27′34′′;8^∘32′57′′).

Solutions

Les solutions sont en cours de développement... Toute solution est la bienvenue.