Résumé : un capitule de tournesol, comme celui d’une pâquerette, ou bien les dispositions des écorces des pommes de pin présentent des familles de spirales qui s’interpénètrent. Le sens d’enroulement étant opposé. Des modélisations permettent de reproduire ce phénomène particulièrement fascinant.
Mots-clés : géométrie, suite, Fibonacci, nombre d’or, modélisation, spirale.
L’exercice s’inspire d’un article publié dans la revue Pour la science no 208 de février 1995, de Ian Stewart, Un peu, beaucoup à la Fibonacci et d’un cours intitulé L’algèbre linéaire à partir d’applications donné par M. A. Robert, aux Etudes pédagogiques de l’enseignement secondaire à Genève en 1996.
Qui n’a pas été fasciné par la régularité des formes géométriques en observant les plantes, les tournesols ou les pétales des pâquerettes. Ainsi, par exemple, on constate que les lys ont 3 pétales, les boutons d’or 5, la plupart des soucis 13, les asters 21, la majorité des composées du type pâquerette 34, 55 ou 89. On trouve rarement d’autres nombres, avec, comme exception les plus notables, les doubles de ces nombres.
Bien sûr, les nombres 3, 5, 8, 13, 21, 34, 55, 89 forment le début de la suite de Fibonacci. Les nombres de Fibonacci furent inventés par un mathématicien italien, Léonard de Pise, dit Fibonacci qui prétendait que la série représentait l’évolution des populations des lapins. Et ces nombres apparaissent dans de nombreux autres domaines. Si l’on observe comment les fleurs de tournesol sont disposées dans la capitule qui les regroupe, on constate que 21 spirales s’enroulent dans le sens des aiguilles d’une montre et 34 dans l’autre sens. Deux nombres de Fibonacci consécutifs une nouvelle fois. Les valeurs exactes dépendent des espèces de tournesols, mais on obtient toujours 21 et 34, 34 et 55, 55 et 89, voire 89 et 144. Les nombres de pétales des pâquerettes sont les mêmes. Les ananas ont 8 rangées d’écailles ; ces parties en losanges s’enroulant vers la gauche et 13 vers la droite. L’épicéa a 5 rangées dans un sens et 8 dans l’autre. Toujours des couples de Fibonacci. Stéphane Douady et Yves Couder de l’Ecole normale supérieure, ont utilisé des modèles informatiques et des expériences de laboratoire pour montrer que la dynamique de la croissance des végétaux expliquait les nombres de Fibonacci et beaucoup d’autres.
Si l’on observe une plante en croissance, on peut reconnaître les pièces qui donneront les principaux organes de la plante : feuille, pétale, sépale, fleuron ou autre. Au centre, se trouve une région circulaire de tissus sans caractéristique spéciale dite apex. Autour de l’apex, une par une, de minuscules excroissances dénommées primordia émergent. Chaque primordium s’écarte de l’apex et, finalement, se transforme en une feuille, un pétale ou autre chose. On peut alors expliquer les formes spiralées et l’existence des nombres de Fibonacci dans les primordia.
La première étape est de concevoir que les spirales les plus apparentes
à l’oeil, les parastiques, ne sont pas fondamentales. La spirale la plus
importante, est engendrée par les primordia dans l’ordre de leur apparition. Les
primordia les plus anciens sont les plus éloignés du centre, de sorte que l’on
peut déduire l’ordre de leur apparition par leur distance à l’apex. Les
primordia sont espacés par une spirale serrée, dite spirale génératrice. Un des
premiers cristallographes, Auguste Bravais, et son frère Louis observèrent
un détail essentiel en 1837. Ils tracèrent les demi-droites qui joignent le
centre de l’apex au centre des primordia et mesurèrent les angles séparant
deux primordia successifs vus de l’apex. Les angles entre les centres des
primordia approchent les 137,5∘. Si l’on prend deux nombres de Fibonacci
consécutifs, par exemple 34 et 55, on obtient la fraction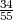 
, on multiplie
par 360∘, on obtient 222,5∘ et des poussières. Si l’on soustrait l’angle,
additionné de 180∘, à 360∘, on obtient 137,5∘. Le rapport de deux nombres de
Fibonacci consécutifs se rapprochent, lorsqu’ils croissent, de plus en plus de
1,618034 qui n’est autre que 
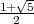, le nombre d’or noté par la lettre grecque
φ.
L’angle d’or α est obtenu en faisant 360 + 360 × (1 - φ) et l’on obtient 137,50776∘. Les frères Bravais observèrent donc que l’angle, entre deux primordia successifs est très proche de l’angle d’or.
Le problème consiste donc à modéliser les capitules des fleurs de tournesol. Pour cela, on disposera des points sur les spirales, on les numérotera, afin de les repérer, puis on représentera les spirales à droite et les spirales à gauche, en fonction des nombres de Fibonacci. Il est conseillé également de tester avec des angles approchant l’angle d’or pour observer le comportement des fleurs de tournesol dans les cas limites.
Pour calculer la position des points sur les spirales, il est conseillé de travailler en
coordonnées polaires. Pour chaque point, le rayon est donné par Rn =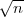 
et
l’angle par φn = n ⋅ α. L’angle α étant l’angle d’or. Il peut être obtenu de
différentes façons. Si l’on appelle φ le nombre d’or, alors α = 2π∕φ2 ou encore
α = 2π∕(φ + 1),α = 2π - 2π∕φ.
La solution actuellement proposée est donnée par les fichiers MatLab : TourneDemo.m, tournesol.m, tournesol.mat et tournesolSimple.m.