Résumé : avec les images de synthèse, on voit de plus en plus de courbes représentées sous la forme d’un tube ou cylindre dont l’éclairage simule l’effet de relief. Les courbes mathématiques peuvent également être représentées, non pas par un trait, mais par un cylindre courbé le long de la courbe. Le but de cet exercice est de définir une fonction permettant d’effectuer de telles représentations.
Mots-clés : géométrie dans l’espace, rotation, produit scalaire, produit vectoriel, translation, dérivée, tangente.
L’énoncé s’inspire des images créées par des ordinateurs et qui représentent des courbes, mathématiques ou non, qui sont enrobées dans un tube ou un cylindre de rayon donné. Avec un éclairage, on peut donner, sur ces représentations, un effet de relief assez réaliste.
Le principe est assez simple : on calcule la tangente à une courbe donnée, puis on construit des cercles perpendiculaires à la direction donnée par la tangente. Ces cercles sont ensuite reliés entre eux par des segments de droites. La surface ainsi définie peut ensuite être colorée, représentée en perspective, etc.
Pour illustrer ce type de représentation, on considérera plusieurs exemples. Le premier exemple consiste à représenter la couture d’une balle de tennis. Celle-ci, en effet, peut être décrite par une fonction en x, y et z donnant la position dans l’espace des points formant la couture d’une balle de tennis. Il faut savoir que celle-ci est définie, afin de permettre, d’abord, la construction de la balle et, ensuite, assurer la meilleure résistance aux chocs lorsque la raquette de tennis frappe la balle.
L’équation est donnée ci-dessous :
![[ π π ]
x = λ a cos(θ + --)- bcos 3(θ + --)
[ 4π 4π ]
y = μ a sin(θ + --)+ bsin3(θ + -)
4 4
z = csin(2 θ)
où
λ = 1+ d sin(2θ)
μ = 1- d sin(2θ)](am160x.png)
Le paramètre θ = 2πt, 0 ≤ t ≤ 1. Dans l’exemple on a pris : a = 1, b = 1, c = 2 et d = 0.
Le deuxième exemple consiste à représenter une courbe dans l’espace que l’on appelle noeud et qui est définie par les équations ci-dessous. Pour définir la courbe on utilise des équations paramétriques (ici le paramètre est donné par la lettre t) : x(t), y(t) et z(t).
Les équations sont les suivantes :
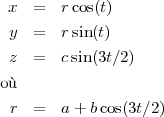
On peut prendre à titre indicatif : a = 1, b = 0.4 et c = 0.5. Le diamètre du tube est d = 0.3.
Le troisième exemple consiste à représenter une courbe de Hilbert dans l’espace. La courbe de Hilbert est une courbe particulièrement intéressante mathématiquement, car, dans sa version originale, dans le plan, elle permet de remplir un carré par une seule courbe. Cette fonction peut également être transposée dans l’espace. On obtient, dans ce cas-là, une courbe magnifique. Si l’on ajoute la possibilité de représenter un cube autour de cette courbe, on obtient le résultat ci-dessous.
L’exemple est donné dans un livre très intéressant qui s’appelle The algorithmic beauty of plans de Przemyslaw Prusinkiewicz et Aristid Lindenmayer et qui utilise les définitions de règles et d’axiomes permettant d’indiquer un comportement à une tortue qui dessine les courbes.
Le problème consiste donc à définir une fonction permettant de représenter un tube ou un cylindre courbé le long d’une courbe donnée par des coordonnées x, y et z puis de définir des fonctions permettant de représenter la couture de la balle de tennis, un noeud dans l’espace et une courbe de Hilbert à 3D.
Pour résoudre ce problème, il est conseillé de définir une fonction qui, étant donné les coordonnées x, y et z un rayon r — c’est le rayon du cylindre qui va parcourir la courbe donnée — et un nombre de sommets permettant de représenter, avec plus ou moins de qualité, le cercle. Il faut faire attention de ne pas prendre un nombre trop élevé. En effet, le cercle qui enrobe une fonction dans l’espace sera plus agréable à la vision, à la représentation, si le nombre de points est relativement faible. Il est conseillé de prendre par défaut 12 points pour créer un cercle.
La méthode conseillée consiste donc à construire des cercles normaux à chaque segment tangent à la courbe. On construira un vecteur tangent à la courbe. Il suffit de considérer, de façon très simpliste, 2 points de coordonnées successives le long de la courbe et de construire le vecteur correspondant. A partir de ce vecteur, on peut définir les angles de rotation permettant d’obtenir un cercle perpendiculaire à ce segment. A partir du moment où l’on a les cercles perpendiculaires à chacun de ces segments, tangents aux courbes, le tube est en fait construit. Mais, il y a un petit problème au niveau de la représentation. En effet, afin d’éviter que les courbes ne se croisent et forment une sorte de nœud papillon, il est indispensable de faire en sorte que les points les plus bas des cercles soient ajustés les uns en face des autres. Donc, il est conseillé, par la suite, de faire tourner les cercles, afin que chacun coïncide exactement avec le précédent.
Pour dessiner la couture de la balle de tennis, il suffit de prendre comme définition des fonctions données plus haut. On peut procéder de la même façon pour le nœud.
Pour modéliser une tortue à 3D, on considère son orientation donnée par trois
vecteurs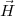 
, 
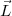et 
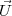indiquant la direction de la tortue. Ces trois vecteurs sont de
longueur 1 et perpendiculaires à chacun :
Les rotations de la tortues sont exprimées par l’équation :
![[ ] [ ]
⃗H ′L⃗′U ⃗′ = H⃗⃗L ⃗U R](am165x.png)
où R est une matrice de rotation 3 × 3. Une rotation d’un angle α autour des
vecteurs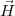 
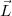et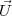 
est donnée par les matrices :
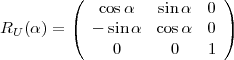
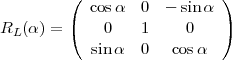
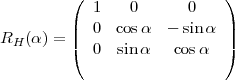
Les symboles suivants contrôlent l’orientation de la tortue dans l’espace.
Pour décrire les courbes dans l’espace, il faut définir un axiome A, puis des règles de réécriture dans lesquelles chaque symbole est remplacé par une suite de symboles. Les seuls symboles autorisés sont : F et f pour avancer (forward) avec trait ou sans, +, -, &, ∧, \, ∕, | pour les rotations comme décrit ci-dessus. Parfois, on utilise les symboles : A (rouge), B (bleu), C (vert) et D (jaune) pour indiquer le changement de couleur.
La courbe de Hilbert dans l’espace est définie par l’axiome et les règles suivants :
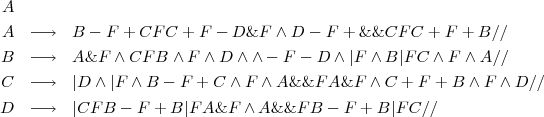
Le nombre d’itérations est donné par n (ici n = 2). L’angle de rotation δ = 90∘.
La solution actuellement proposée est donnée par les fichiers MatLab : TubeDemo.m, ver3.m, tennis.mat, Hilbert3D.m, reecriture.m, MatRotDef.m et Tortue3D.m.