Résumé : les mathématiques peuvent être plaisantes lorsqu’elles sont au service de l’esthétique. La création de cartes de vœux fractales peut avoir deux utilisations évidentes : les entreprises qui veulent utiliser cette idée pour leurs cartes de vœux et les enseignants qui souhaitent l’expliquer à leurs élèves tout en faisant des mathématiques intéressantes.
Mots-clés : fractal, triangle de Pascal, coefficients binômiaux, numération binaire.
L’exercice s’inspire de l’article de Peter Hilton, Jean Pedersen et Hans Walser publié dans la revue The Mathematical Gazette No 491, Volume 81, juillet 1997.
On désire réaliser une structure fractale à l’aide d’une feuille de papier. Ce qui peut motiver la plupart des gens à réaliser ce genre d’objet, c’est essentiellement son aspect esthétique. En réalité, cet exercice a deux utilisations évidentes. D’abord, les entreprises fabriquant les cartes postales peuvent y trouver des idées intéressantes pour réaliser des cartes de vœux en 3 dimensions qui tiennent aisément dans une enveloppe et, deuxièmement, les enseignants qui désirent expliquer à leurs élèves comment les fabriquer (et ceci en apprenant de belles mathématiques).
La structure est un modèle pour une étape dans un processus d’auto-similarité conduisant à une fractale. La construction du modèle consiste à découper une feuille de papier et ensuite à plier des segments de droite comme des «montagnes» et les autres comme des «vallées». Le résultat est donné dans la figure ci-dessous.
Pour construire un modèle, on commence avec une feuille de papier (ou du carton mince). La figure ci-dessous montre le schéma des traits de coupe, de plis en montagne et de plis en vallée. Les zones grises seront les surfaces verticales et les zones plus sombres les surfaces horizontales. Après avoir dessiné le schéma, il suffit de découper les traits pleins avec un cutter, et de préparer les plis avec un objet pointu (non coupant)1 . Il reste l’étape la plus difficile : plier selon les plis et maintenir la carte à 90∘. On peut utiliser une astuce : on maintient les plis les plus petits avec des cure-dents.
Il est conseillé de s’exercer en recopiant le modèle et en s’entraînant sur des versions simplifiées (cartes de vœux de niveau 2, par exemple). On peut coller la feuille de papier sur un support plus rigide. On marquera les extrêmités des traits en les perforant ; on utilisera ensuite un cutter pour découper les traits verticaux. Pour marquer les plis on peut utiliser un os de pliage ou un stylo (sans encre). Cette partie est longue et ennuyeuse mais elle permet de contempler la régularité et les propriétés fascinantes du triangle de Pascal...
Le but de l’exercice est de représenter des cartes de vœux fractales. La généralisation doit également être prise en compte : niveau quelconque, généralisation et raisonnement sur la base 3, etc.
Lorsque l’on a plié pour la première fois une telle carte postale, on constate quelques évidences. Si on l’observe de côté, on repère rapidement la nature fractale de la carte. On peut définir les quatres premières étapes suivant le schéma ci-dessous.
La figure F0 est la figure génératrice à l’étape 0. On part d’un carré. La règle pour passer de l’étape n à l’étape (n + 1) est la suivante : prendre les carrés les plus petits introduits à l’étape n et attacher à chacun 3 carrés additionnels avec des côtés (dont la longueur est la moitié de la longueur du côté de l’étape n) aux emplacements suivants :
On observe ainsi le passage de F2 à F3. En principe, le processus peut être poursuivi indéfiniment, mais il n’est pas possible en revanche de construire la fractale finale F = limk→∞Fk. On observe également que le résultat ressemble au tapis de Sierpinsky même s’il est construit différemment.
En rajoutant une dimension on peut imaginer de petits cubes empilés et on obtient la carte postale dessinée plus haut.
On peut trouver une relation entre les étapes de construction de cette fractale avec les nombres binaires : on adopte la convention que si l’on peut représenter tous les nombres entiers inférieurs à 2n+1, alors on donnera aux arêtes du cube original une longueur 2n. Par exemple, si l’on prend n = 3, on part d’un cube dont les arêtes sont de longueur 8, F0 et on poursuit en ajoutant les étapes F1 (cubes d’arêtes 4), F2 (cubes d’arêtes 2) et F3 (cubes d’arêtes 1).
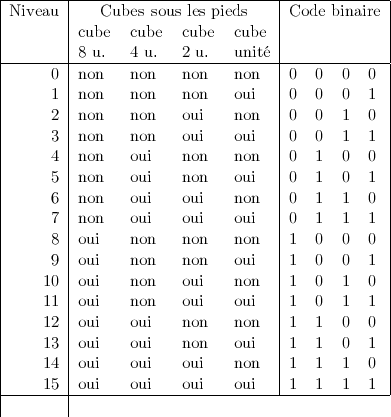
Si l’on numérote les cubes comme ci-dessus le long de l’escalier, on constate qu’au niveau 1 on a un cube d’une unité, au niveau 2 on a 1 cube de deux unités, au niveau 3 on a 1 cube d’une unité et 1 cube de deux unités, etc. Ceci est connu : il s’agit de l’écriture des nombres en base 2. On peut résumer cette propriété par le tableau ci-dessous.
On peut se poser d’autres questions : quelle est la limite du volume lorsque n croît et quelle est-elle pour la surface ?
On peut également trouver une ressemblance avec le triangle de Pascal. En observant la carte de vœux (on peut la couper en deux et la tourner de 90∘), on constate que les vallées correspondent aux nombres impairs du triangle de Pascal. On peut même généraliser et considérer les restes en base n, on obtient, là également, de magnifiques carte de vœux.
Le processus de l’escalier est recommandé : on compte le nombre de cubes sous ses pieds à chaque marche en adoptant alors le système de numération en base n. On observera aisément l’emplacement des vallées.
La solution actuellement proposée est donnée par les fichiers MatLab : CarteVoeuDemo.m, param.m, aidefun.m, cartepr.m, cartepp.m, voeu.m, carreor.m et carreop.m.