Résumé : les carrés magiques sont connus de tous. Une nouvelle race de carrés magiques a été inventée par un expert des jeux de mots, Lee C. F. Sallows : les carrés alphamagiques. Ces carrés magiques sont écrits en toutes lettres et les longueurs des mots sont également des carrés magiques. Dans chaque langue on en trouve d’autres. Pourquoi ne pas essayer de découvrir des carrés alphamagiques orthographiés en français tout en respectant les particularismes romands (huitante, etc.) ?
Mots-clés : carré magique, progression arithmétique, linguisitique, carré latin, carré gréco-latin.
L’exercice s’inspire de l’article Alphamagic Squares, Adventures with turtle shell and yew between mountains of mathematics and the lowlands of logology de Lee C. F. Sallows, The lighter side of Mathematics, Richard Guy et Robert Woodrow, Mathematical Association of America, 1994 et de l’article Les carrés alphamagiques, Les beautés des carrés magiques, numériques et linguistiques de Ian Stewart, Pour la Science, No232 février 1997.
L’histoire des carrés magiques est considérable et nous ramène aux légendes de la Chine ancienne. Ainsi, le carré magique le plus réputé, le plus simple et le plus vieux est sans doute le carré magique appelé Lo shu (shu signifie écrire, document). La légende raconte qu’il a été révélé sur le dos d’une tortue sacrée apparue à l’empereur mythique Yü au XXIIIe siècle avant J.-C.
En fait, la sinologie moderne identifie ces signes comme une pseudo-invention datant du dixième siècle après J.-C. La traduction en chiffres arabes est donnée à droite.
Le dos de la tortue devait ressembler à :
La plupart des lecteurs savent que la propriété magique de ces carrés réside dans le fait que la somme des lignes, des colonnes et des diagonales est la même. La littérature regorge de curiosités sur les carrés magiques : triangles, rectangles, cercles, étoiles magiques, carrés antimagiques, carrés de nombres premiers, carrés magiques au produit, cubes et tableaux de dimension n magiques, etc. En revanche, il reste des questions en suspens : combien de carrés magiques distincts et consécutifs existe-t-il pour des dimensions supérieures à 5 × 5 ?
Un développement inattendu a vu le jour en 1985 lors de la redécouverte d’un
ouvrage The origin of Tree Worship mettant à jour un parallèle entre un épisode
du règne de Roi M
, un chef de tribu de Bretagne du Nord, et la légende
chinoise du Lo shu. Ce livre a disparu et réapparu mystérieusement en
1985.
Parmi les mythes celtes narrés dans cet ouvrage, il y a la narration d’un
pèlerinage effectué par le Roi M
vers une grotte sacrée, à 
ohdalir, Vallée des
Ifs, où une formule magique lui fut révélée. Cette figure peut être écrite en
anglais de la façon suivante :
Fasciné par la similitude entre cette découverte et le carré magique de Li shu, Lee C. F.Sallows, constatant que le nombre de runes1 et le nombre de lettres en anglais était le même, a réécrit le carré magique ci-dessus en comptant la longueur des mots. La surprise est d’autant plus grande que l’on obtient également un carré magique :
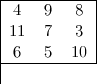
Plus encore, c’est le plus petit carré magique que l’on peut trouver, puisque les nombres en anglais ne peuvent pas avoir moins de trois lettres. Ces étonnements ont conduit Lee C. F. Sallows à rechercher d’autres carrés alphamagiques.
Alphamagique est le qualificatif utilisé pour décrire n’importe quel carré magique (carré, rectangulaire, triangulaire, de dimension n) qui reste magique lorsque toutes les entrées ont été remplacées par des nombres représentant la longueur du mot, en lettres, dans leur écriture conventionnelle (ainsi deux devient 4). Naturellement, un carré qui est alphamagique dans une langue ne l’est pas nécessairement dans une autre (les langues non alphabétiques n’ont pas de sens dans ce contexte).
On utilisera la convention suivante pour nommer la longueur des nombres écrits en lettres : le logorithme ou log d’un nombre (logos = mot, arithmos = nombre). Le logorithm ne doit pas être confondu avec le mot ressemblant imaginé par l’Ecossais Napier en 1614 : le logarithme. Lorsque cela n’est pas précisé, on utilisera les ”log naturels” ou log e(nglish) ; ainsi log 15 + log 3 = log français69 puisque 7 + 5 = 12, le nombre de lettre de soixante-neuf.
On qualifiera de magique n’importe quel arrangement produisant une somme constante le long des orthogonales et des diagonales, sans exiger des éléments distincts ou non. Naturellement, un carré avec des entrées répétées est moins intéressant que celui dont tous les éléments sont différents. L’ordre d’un carré magique est défini par sa taille (le nombre de cellules sur un côté). Le Li shu est donc un carré alphamagique anglais d’ordre 3, ayant comme autres propriétés que ses logorithmes sont tous différents, consécutifs et qu’il est minimal.
Pour pénétrer ce terrain peu familier, il est naturel d’observer les carrés alphamagiques d’ordre 3 (3 × 3). Il est utile alors de considérer la formule générale établie par Édouard Lucas, mathématicien français du XIXe siècle :
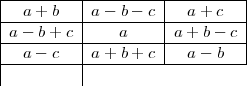
Comme les nombres et leurs logorithmes doivent satisfaire ces relations, cette formule mérite toute l’attention : trois éléments dans chaque ligne passant par le centre forment une progression arithmétique, c’est-à-dire que deux termes consécutifs diffèrent d’une constante ((a - b + c) - a = a - (a + b - c), par exemple). La première étape consiste donc à rechercher uniquement les triplets d’entiers en progression arithmétique tels que les logorithmes soient également en progression arithmétique.
Le figure ci-dessous affiche la liste des nombres cardinaux de 0 à 28 avec leurs logorithmes anglais :
Choisissons, par exemple, 15 comme nombre central, puisque nous savons qu’un tel carré alphamagique existe. La table des logorithmes révèle cinq triplets adéquats : (2,15,28), (5,15,25), (8,15,22), (11,15,19) et (12,15,18) ; les logorithmes sont alors : (3,7,11), (4,7,10), (5,7,9), (6,7,8) et (6,7,8).
Il faut alors essayer toutes les paires possibles de ces triplets, par exemple, sur les diagonales. Ainsi, avec les deux premiers, nous avons :
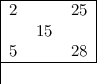
La formule de Lucas nous dit que le nombre manquant en haut peut être calculé simplement en prenant la constante magique (trois fois le nombre du centre = total des orthogonales et des diagonales) moins les termes latéraux. Ici, le nombre du haut est : (3 × 15) - (2 + 25) = 18. Ce raisonnement peut être appliqué aux autres cellules manquantes et on obtient :
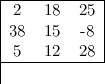
Ce carré doit être rejeté à cause du nombre négatif -8 (qui aurait pu être écrit ”minus eight”, mais alors le carré magique dérivé formé des logorithmes n’aurait pas été magique).
Evidemment, on peut résoudre ce problème à la main avec un peu de patience. Le Li shu sera trouvé rapidement. Pour chercher d’autres carrés alphamagiques d’ordre 3, il est alors souhaitable d’utiliser un ordinateur et de chercher un algorithme suffisamment général pour être appliqué à d’autres langues.
Le but de ce problème est donc de rechercher des carrés alphamagiques pour de nombreuses langues et, comme l’orthographe est prépondérante, de considérer également des particularismes locaux. Ainsi, en Suisse et en Belgique, on utilise huitante, nonante, alors qu’en France on dit quatre-vingts et quatre-vingt-dix.
La méthode pour rechercher des carrés alphamagiques a été donnée dans l’énoncé. Pour la langue anglaise, Lee C. F. Sallows a orthographié les nombres 101, 102, etc. comme suit : one hundred one et one hundred two. Le guide du typographe romand indique quant à lui : one hundred and one et one hundred and two, ce qui change évidemment les logorithmes. Pour tester, il est conseillé de travailler comme l’inventeur.
En particulier, il sera intéressant de trouver les carrés alphamagiques et leurs harmoniques. Ces derniers peuvent être obtenus à partir d’un carré précédent. Ainsi le Li shu peut donner un carré alphamagique très simple en ajoutant one hundred à chaque nombre. Cela revient à ajouter 10 (le logorithme de one hundred aux logorithmes du Li shu. Il est intéressant de rechercher également des carrés alphamagiques dont les logorithmes sont des nombres consécutifs (par exemple, les carrés dont les constantes sont : (885;60) et (897;60)).
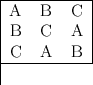
Les carrés latins, gréco-latins ou eulériens méritent également d’être étudiés. Un carré latin est un carré dont les trois mêmes nombres apparaissent dans chaque ligne et chaque colonne (de sorte que colonnes et lignes ont les mêmes sommes) :
Un carré gréco-latin est formé en superposant deux carrés latins de telle sorte que chaque cellule est occupée par une entrée différente. Le terme dérive de la pratique consistant à mélanger des lettres romaines et grecques pour distinguer les composants ; ce type de carré a été étudié par Leonhard Euler. On peut démontrer que l’ordre 3 admet une seule possibilité (en combinant une paire de carrés latins, il n’est pas nécessaire d’additionner leurs éléments, mais de les accoler) :
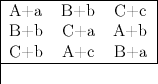
ou
On observera le carré (162;27). On constatera également qu’ajouter 1 à ce carré en produit un autre. On peut trouver 16 carrés adjacents de ce type jusqu’à 100. De plus, si l’on prenait le logorithme d’un logorithme, obtiendrait-on un carré magique ? Peut-on également trouver un carré magique auto-reproducteur ?
En français, Lee S. C. Sallows ne trouve qu’un carré alphamagique inférieur à 200, mais 255 autres si les éléments peuvent aller jusqu’à 300. Trois d’entre eux ont pour logorithme neuf entiers consécutifs. Si l’on orthographie les nombres selon les règles en usage dans la langue française, on obtient en réalité, 4 carrés alphamagiques n’utilisant que des nombres inférieurs à 200 et 252 carrés alphamagiques dont les éléments peuvent aller jusqu’à 300.
En allemand, il n’y a pas moins de 221 exemples utilisant des nombres inférieurs à 100. Le principe de base de construction se comprendra si l’on extirpe les syllabes ”und” et ”zig” et remplace les mots restants par des nombres. L’exemple ci-dessous est intéressant :
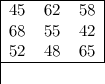
En allemand, cela donne :
On peut également séparer les dizaines des unités pour obtenir deux carrés latins.
On peut enfin également s’intéresser aux ordres supérieurs, aux carrés normaux (formés d’entiers consécutifs), aux cubes alphamagiques, au dérivé d’un carré, etc.
L’écriture des nombres dans d’autres langues est formatrice également. On pourra essayer l’italien, le latin, etc. Lee C. F. Sallows donne des exemples également en swahili, suédois, etc.
Un exemple en latin :
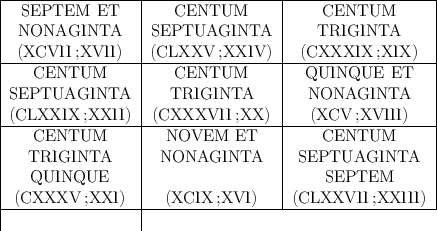
Un exemple en italien :
La solution actuellement proposée est donnée par les fichiers MatLab : alphaAnglais.m, anglais.mat, demoAlpha.m, logorithme.m et alphamagique.m.