Résumé : les polyèdres ont de tout temps fasciné les mathématiciens. Ces objets ont une certaine forme de perfection. Rien d’étonnant à ce qu’on les trouve dans les structures cristallines. Comment peut-on alors trouver les cinq polyèdres réguliers, puis leurs dérivés semi-réguliers et enfin les polyèdres étoilés ?
Mots-clés : harmonie, géométrie, sphère, symétrie, barycentre.
L’exercice s’inspire de l’article La musique des sphères de Marc-Lachièze Rey et Jean-Pierre Luminet, Pour la science No 253, novembre 1998.
Pour les Pythagoriciens, l’Univers devait nécessairement se manifester par des proportions « justes », par des rythmes, par des nombres : le monde chantait et vibrait harmonieusement. (...) Considérant le cosmos dans son ensemble comme un système harmonieux, ils en avaient déduit que les sept notes naturelles de la gamme étaient en correspondance avec les sept corps célestes connus (le Soleil, la Lune et les cinq planètes visibles) auxquelles s’ajoutaient trois sphères supplémentaires pour atteindre le nombre dix, parfait entre tous (car c’est notamment la somme des quatre premiers entiers).
Un peu plus tard, au IVe siècle, Platon décrit, dans l’Epinomis, cette harmonie céleste, en déclarant notamment que les astres exécutent « le plus magnifique de tous les chœurs ». (...) Cette tradition, assimilant le cosmos à un instrument de musique, se perpétue pendant le Moyen Âge et jusqu’à la Renaissance scientifique. (...) Pour le Français Marin Marsenne, tout ce qui s’exprime par des proportions peut être traité en termes d’harmonie et donc, en particulier, la disposition des orbes célestes. A la même époque, l’astronome allemand Johannes Kepler reprend l’idée qu’un astre émet un son d’autant plus aigu que son mouvement est rapide, et l’adapte à sa découverte de la nature elliptique des orbites planétaires : des intervalles musicaux bien définis sont associés aux planètes.
Dans le Secret du monde, ouvrage rédigé à l’âge de vingt-cinq ans, Kepler expose une vue générale sur l’Univers fondée sur les solides parfaits. Il inscrit un octaèdre entre les orbites de Mercure et de Venus, un icosaèdre entre Venus et la Terre, un dodécaèdre entre la Terre et Mars, un tétraèdre entre Mars et Jupiter, et un cube entre Jupiter et Saturne. Après de nombreux calculs, Kepler voit « les solides symétriques s’insérer les uns après les autres avec tant de précision entre les orbites appropriées que si un paysan demandait à quels crochets les cieux sont fixés pour ne pas tomber, il serait facile de lui répondre ». (...) En février 1596, Kepler se rend à la cour de son protecteur, le duc Frédéric de Wurtemberg, pour le persuader de faire construire une maquette de l’Univers en forme de coupe. Les symboles des planètes seraient taillés dans des pierres précieuses : un diamant pour Saturne, une hyacinthe pour Jupiter, une perle pour la Lune, etc. La coupe verserait plusieurs brevages, que des tuyaux dissimulés amèneraient de chaque sphère planétaire à sept robinets placés sur le rebord. Le projet n’aboutit pas.
Les polyèdres sont très bien décrits dans le livre Mathematica dans les lycées de Robert Cabessa, Loisirs et pédagogie, Lausanne 1996.
Des Egyptiens, avec leurs pyramides, aux réalisations architecturales modernes, nous pouvons parcourir les siècles en présentant quelques maîtres à penser, chercheurs, artistes dont les noms sont associés aux polyèdres.
On attribue leur découverte à Pythagore (VIe siècle avant J.-C.) et ses disciples. Hiéroclès, Archytas, Philoläus pour le cube, le tétraèdre et le dodécaèdre, Théétète pour l’octaèdre et l’icosaèdre. Il n’existe que cinq polyèdres réguliers.
Platon (428-348 avant J.-C.), illustre philosophe grec, associe les polyèdres aux éléments naturels. Le Feu au tétraèdre, l’Air à l’octaèdre, la Terre au cube, l’Eau à l’icosaèdre et coiffant le tout, l’Univers au dodécaèdre. Les polyèdres réguliers sont aussi appelés corps de Platon.
(...) Archimède (287-212 avant J.-C.) démontra qu’à partir des cinq polyèdres réguliers on ne peut construire que treize polyèdres semi-réguliers (en fait quinze si l’on rajoute les prismes et antiprismes) qu’on appelera désormais polyèdres archimédiens.
Léonard de Vinci (fin du XVe siècle), a dessiné de nombreux polyèdres réguliers, semi-réguliers ou irréguliers. Ces dessins furent exécutés à la demande du grand mathématicien Luca Pacioli, pour son ouvrage « De divina proportione » (1496). Ils se caractérisent par une grande précision scientifique.
Euler, mathématicien suisse (1707-1783) établit la formule F + S = A + 2 où F est le nombre de faces du polyèdre, S le nombre de sommets et A le nombre d’arêtes.
Plus proche de nous, Escher (1898-1971), s’est passionné pour les dessins géométriques, fausses perspectives et illusions d’optique. Au début de sa carrière, seuls les mathématiciens, cristallographes et physiciens témoignaient de l’intérêt pour ses travaux. Ecoutons-le : « Très longtemps avant l’apparition de l’homme sur terre, des cristaux s’étaient déjà formés dans la croûte terrestre. Un beau jour, l’homme vit pour la première fois un tel morceau à formes régulières ... et s’étonna ».
Effectivement les structures régulières ou irrégulières se retrouvent dans la nature sous forme de cristaux ou dans des structures végétales ou animales. On peut rencontrer des octaèdres naturels de fluorine ou des dodécaèdres parfaits de pyrite.
Le but du problème est de construire les polyèdres réguliers, semi-réguliers et étoilés avec des représentations graphiques rappelant Kepler et de Vinci.
On appelle polyèdre régulier toute figure de l’espace délimitée par des polygones tels que, quel que soit un côté du polygone, il existe deux polygones et deux seulement ayant ce côté en commun. Les polygones sont les faces du polyèdre, les segments communs à ces faces les arêtes. On appelle polyèdre régulier convexe tout polyèdre dont toutes les faces sont des polygones réguliers convexes égaux. Il en résulte qu’il existe deux sphères de même centre, l’une inscriptible au polyèdre et l’autre circonscriptible. Rappelons qu’il n’existe que cinq polyèdres réguliers convexes.
Il y a plusieurs façon de le démontrer. Nous choisirons celle-ci : soit s un sommet du polyèdre fait de polygones réguliers P et i le nombre d’arêtes aboutissant en s (i est aussi le nombre de polygones de sommet commun s). La somme des angles en s doit être strictement inférieur à 360∘.
Si P est un triangle équilatéral, alors i × 60∘ < 360∘, donc i < 6. Si i = 3, alors on a un tétraèdre, si i = 4, on a un octaèdre, si i = 5 il s’agit de l’icosaèdre.
Si P est un carré, alors i × 90∘ < 360∘, donc i < 4. Si i = 3, on obtient le cube.
Si P est un pentagone, alors i× 108∘ < 360∘, donc i ≤ 4. Si i = 3, on obtient un dodécaèdre.
Si P est un hexagone, alors i× 120∘, donc i < 3. Or ceci est impossible. Si le nombre de côtés du polygone dépasse cinq, il n’existe aucun polyèdre régulier correspondant.
Pour définir le tétraèdre régulier, il suffit de le placer comme ci-dessous.
On prend les sommets T2, T3 et T3 dans un plan horizontal d’équation
z = -c(c > 0). Alors, T2(2a,0,c) est un des sommets. Par rotation de T2 autour
de l’axe Oz d’angles respectifs 2π∕3 et 4π∕3, on obtient T3(-a,a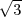 ,-c) et
T4(-a,-a
,-c) et
T4(-a,-a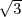 ,-c). Le premier sommet T1 est sur l’axe Oz et sa cote vaut 3c car
l’origine est au 3∕4 de la hauteur issue de T1 (propriété géométrique du centre de
gravité d’un tétraèdre). En égalant les longueurs de T1T4 et T3T4 on
a :
,-c). Le premier sommet T1 est sur l’axe Oz et sa cote vaut 3c car
l’origine est au 3∕4 de la hauteur issue de T1 (propriété géométrique du centre de
gravité d’un tétraèdre). En égalant les longueurs de T1T4 et T3T4 on
a :
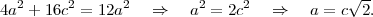
Le milieu I de T3T4 étant placé sur une sphère de rayon 1, on a :
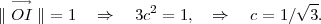
Les sommets sont donc : T1(0,0,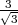 ), T2(2
), T2(2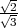 ,0,-
,0,-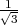 ), T3(-
), T3(-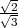 ,
,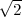 ,-
,-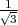 ) et
T4(-
) et
T4(-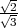 ,-
,-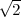 ,-
,-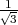 ).
).
Pour définir l’octaèdre régulier, il suffit de le placer comme ci-dessous. Pour
s’assurer d’une sphère circonscrite de rayon 1, il faut prendre les sommets
suivants : O1(0,0,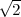 ), O2(
), O2(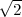 ,0,0), O3(0,
,0,0), O3(0,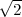 ,0), O4(-
,0), O4(-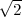 ,0,0), O5(0,-
,0,0), O5(0,-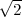 ,0),
O6(0,0,-
,0),
O6(0,0,-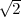 ).
).
Pour définir l’hexaèdre régulier (ou cube, ou dé), il suffit de l’observer de face
et de dessus. Pour s’assurer d’une sphère circonscrite de rayon 1, il faut que la
distance de l’origine au milieu des arêtes soit égale à 1 (donc une demi arête est
égale à sin(π∕4) = 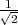 ). On a alors les sommets suivants : H1(a,a,a),
H2(-a,a,a), H3(-a,-a,a), H4(a,-a,a), H5(a,a,-a), H6(-a,a,-a),
H7(-a,-a,-a) et H8(a,-a,-a), où a = 1∕
). On a alors les sommets suivants : H1(a,a,a),
H2(-a,a,a), H3(-a,-a,a), H4(a,-a,a), H5(a,a,-a), H6(-a,a,-a),
H7(-a,-a,-a) et H8(a,-a,-a), où a = 1∕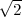 .
.
Pour définir l’icosaèdre régulier, on peut remarquer qu’il y a trois plans de symétrie perpendiculaires deux à deux contenant chacun quatre sommets disposés en rectangle. Chaque sommet est équidistant de cinq sommets. L’icosaèdre reste invariant par rotation d’angles multiples de 2π∕5 autour d’un quelconque de ses six axes passant par deux sommets opposés. Il existe donc 12 plans contenant cinq sommets et parallèles deux à deux.
Les douze sommets sont alors définis par (0,±T,±1), (±1,0,±T) et
(±T,±1,0) où T est le nombre d’or (T = 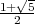 ).
).
Il y a d’autres façons de définir l’icosaèdre : on calcule les coordonnées des sommets à partir des propriétés des triangles équilatéraux et du nombre d’or. On peut également raisonner comme suit : on place deux sommets sur l’axe Oz ; d’un de ces deux sommets, on trace une sphère de rayon égal à l’arête L du polyèdre considéré. Le polyèdre est inscrit dans une sphère de rayon 1. On construit alors le plan d’intersection des deux sphères. Les coordonnées se déduisent alors aisément.
Pour définir le dodécaèdre régulier, il suffit de constater que le dodécaèdre est la figure duale de l’icosaèdre en ce sens que ses sommets sont les centres de gravité des faces de ce dernier et réciproquement.
Pour calculer les coordonnées du dodécaèdre, il faut prendre la somme divisée par trois des coordonnées des sommets des faces de l’icosaèdre.
La déduction d’un polyèdre à partir d’un autre était le point de départ de notre exercice. En choisissant correctement les rayons des sphères circonscrites, il est possible de reproduire graphiquement l’emboîtement des polyèdres imaginé par Kepler.
La solution actuellement proposée est donnée par les fichiers MatLab : barycentre.m, cubeCamard.m, cubocatedre.m, democubecamard.m, democubeoctaedre.m, demoPolyRelief.m, faceNouvelle.m, faceTronquee.m, kepler.m, plot3d.m, poly.mat, polyedreEtoile.m, polyedres.m, polyedresSemiReguliers.m et polygoneReduit.m.