Résumé : pour connaître les phases de la lune, quoi de plus parlant qu’un calendrier avec une indication journalière ? Mais comment calcule-t-on les phases de la lune ? A-t-elle (la lune) un comportement régulier ? Pour répondre à ces questions, il suffit de demander à un ordinateur de donner une bonne approximation du mouvement de la lune.
Mots-clés : astronomie, révolution, orbite, période, perturbation.
L’exercice s’inspire du livre Astronomie & Astrophysique de Martin Séguin et Benoît Villeneuve, Masson, Paris, 1995 et des calendriers lunaires publiés dans le commerce.
Le cycle des phases de la lune, c’est-à-dire le changement de son aspect au cours du mois, est l’un des phénomènes astronomiques les plus facilement observables. Déjà, les Grecs de l’Antiquité savaient que la lune est sphérique et qu’elle ne brille pas par elle-même. Ils avaient compris que les parties de la lune qui nous apparaissent lumineuses reflètent la lumière du soleil.
La lune tourne autour de la terre en un mois environ, période au cours de laquelle sa position change par rapport au soleil. Lorsque la lune est diamétralement opposée au soleil, on peut apercevoir de la terre la totalité de sa zone éclairée : il s’agit de la pleine lune. Lorsque la lune passe entre la terre et le soleil, la partie éclairée de la lune n’est pas visible, et c’est la nouvelle lune. Entre ces deux extrêmes, il y a les phases intermédiaires : le croissant, le quartier (demi-lune) et la lune dite « gibbeuse », dont plus de la moitié de la partie éclairée est visible.
Contrairement à une croyance assez répandue, les phases de la lune sont fonction des positions relatives du soleil et de la lune ; elles n’ont rien à voir avec l’ombre de la terre. Pour s’en convaincre, on n’a qu’à observer la forme de la lune gibbeuse : l’ombre circulaire de la terre projetée sur la face éclairée de la lune ne pourrait donner ce résultat ! Néanmoins, il arrive une ou deux fois par année que l’ombre de la terre touche la lune : c’est l’éclipse de lune.
Pour éviter la confusion, les astronomes utilisent deux termes pour décrire les mouvements périodiques. Le mot rotation est réservé au mouvement périodique d’un objet sur lui-même. Par exemple, on peut parler de la rotation de la terre sur elle-même, ou de sa rotation tout court. Lorsque l’on veut désigner le mouvement périodique orbital d’un objet autour d’un autre objet, on utilise le terme de révolution. Par exemple, on parle de la révolution de la terre autour du soleil et de la révolution de la lune autour de la terre.
L’examen de n’importe quel recueil de données astronomiques révèle deux faits intrigants :
Pour comprendre l’origine des légères différences de temps, il faut savoir que le calcul de l’intervalle de temps requis pour qu’un phénomène périodique donné se reproduise (par exemple, l’intervalle entre deux pleines lunes) nécessite souvent la combinaison de différents mouvements périodiques. En effet, notre plate-forme d’observation, la terre, possède deux mouvements périodiques principaux : une rotation sur elle-même et une révolution autour du soleil. Et lorsque nous observons la lune, il faut en plus tenir compte de sa révolution autour de la terre.
Observons la rotation de la terre (sur elle-même) depuis un point immobile dans l’espace, quelque part au-dessus du pôle nord de la planète. Imaginons un bâton planté verticalement dans le sol, à l’équateur. Prenons pour instant 0 le moment où le bâton pointe directement vers le soleil : il est alors midi, heure solaire. Il faudra attendre 23h et 56min avant que le bâton, entraîné par la rotation de la terre ne fasse un tour complet autour du centre de la terre. Mais, pendant ce temps, la terre s’est déplacée autour du soleil, de sorte que le bâton ne pointe pas encore vers le soleil : il n’est pas encore tout à fait midi.
Voyons comment s’explique la différence de 4min entre la durée de la rotation de la terre et la journée de 24h. La terre effectue une rotation autour du soleil (360∘) en un an (365 jours et 1/4). En 23h 56min, presque un jour, elle parcourt environ 1∘ sur son orbite. Ainsi, pour que le bâton revienne vis-à-vis du soleil, il faut que la terre tourne sur elle-même de 1∘ de plus. La terre tourne de 15∘ à l’heure. Pour tourner de 1∘, il lui faut le quinzième d’une heure, soit 4 min. Ainsi, il faut attendre 24h (23h 56min + 4min) pour qu’il soit de nouveau midi, heure solaire, à l’endroit où se trouve le bâton.
Si nos montres étaient réglées sur la véritable rotation de la terre par rapport à un point fixe, d’une durée de 23h 56min, le soleil ne culminerait pas toujours dans le ciel à la même heure. Il serait parfois midi le matin, midi le soir ou midi en pleine nuit. En réglant nos montres d’après un cycle de 24h, on maintient la concordance entre l’heure et le cycle du jour et de la nuit.
Les astronomes nomment jour sidéral (du latin sideris, ”astre”) le cycle de 23h 56min, parce que celui-ci se rapporte à la rotation de la terre mesurée par rapport à l’ensemble des étoiles du ciel pris comme système de référence. Le cycle de 24h se nomme jour solaire.
Observons maintenant, du même point de vue, la révolution de la lune autour de la terre, qui se meut elle-même autour du soleil. Prenons pour instant 0 le moment de la plein lune : par rapport à la terre, la lune est alors diamétralement opposée au soleil. La lune fait une révolution autour de la terre en 27,3 jours, c’est-à-dire en un mois sidéral. Mais, pendant ce temps, la terre se déplace d’environ 27∘ de plus sur son orbite. Ainsi, au bout d’un mois sidéral, ce n’est pas encore la pleine lune. La lune doit parcourir environ 27∘ de plus sur son orbite pour être de nouveau diamétralement opposée au soleil (comme la terre se déplace elle-même pendant ce mouvement, le parcours supplémentaire s’allonge encore un peu, à environ 29∘). Puisque la lune parcourt 13∘ par jour (360∘∕27,3 jours), il lui faudra un peu plus de deux jours. Et ainsi, après 29,5 jours, c’est-à-dire après un mois synodique (du grec sunodikos, ”conjonction”), ce sera de nouveau la pleine lune. Le cycle des phases de la lune est donc plus long de 2,2 jours que sa période sidérale.
Fait intéressant, la période de rotation de la lune (sur elle-même) est également de 27,3 jours. C’est pourquoi elle présente toujours la même face à la terre.
Pour réaliser un calendrier lunaire, il semblerait qu’il suffise de prendre une date exacte de pleine lune ou de nouvelle lune, puis d’ajouter systématiquement 27,3 jours. Comme on ne peut négliger les perturbations dues au soleil, le calcul exact des phases de la lune et, par conséquent, des dates des éclipses est relativement difficile. Une formule est donnée plus bas dans les indications.
Le problème consiste donc à représenter un calendrier lunaire pour une année précise. On trouvera ci-dessous un exemple pour 1999 :
On recommande de calculer avec précision l’heure de la nouvelle lune et de déduire ensuite les autres phases de la lune pour une année. Les indications données ci-dessous sont extraites du livre Astronomy On The Personal Computer par Olivier Montenbruck et Thomas Pfleger, Springer-Verlag, 1994. Elles sont parfois trop complexes pour être détaillées. On recommande la lecture du livre pour le détail.
L’heure de la nouvelle lune est donnée par l’instant où les longitudes du soleil (λ⊙) et de la lune (λL) sont identiques, c’est-à-dire la différence (λ⊙- λL) disparaît. La formule tient compte de la différence D entre les longitudes moyennes plus la différence entre les perturbations périodiques :
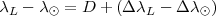
La différence D est donnée par :
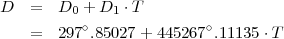
où T est :
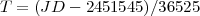
JD est le jour dans le calendrier julien ; il donne le nombre total de jours qui se sont écoulés depuis 4713 avant Jésus Christ (1 janvier). Le nom vient de Julius Scaliger, le père de Josephus Justus Scaliger, qui fut le premier à l’utiliser pour des besoins en astronomie.
D1 indique le changement total de D pendant un siècle julien. L’intervalle moyen entre deux nouvelles lunes, c’est-à-dire le temps pendant lequel D varie de 360∘, est approximativement 29,53 jours.
Les perturbations périodiques des orbites lunaires et solaires varient peu pendant une période courte (Δt). L’approximation t0 pour l’heure de la nouvelle lune peut alors être améliorée en utilisant :
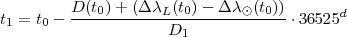
Si cette étape est répétée, alors l’heure de la nouvelle lune est relativement bonne. ΔλL et Δλ⊙ peuvent être calculés par des séries tenant compte des longitudes et des perturbations du soleil et de la lune :
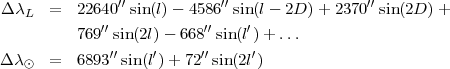
l et l′ sont les anomalies moyennes pour la lune et pour le soleil. Imaginons un corps hypothétique tournant d’un mouvement régulier autour du Soleil, d’un pas n par unité de temps. Entre le passage au périhélie et le moment t, ce corps aura tourné d’un angle μ = n(t - t0), cet angle est appelé anomalie moyenne et le pas n est une des caractéristiques de la planète.
La solution actuellement proposée est donnée par les fichiers MatLab : NouvLune.m, caldat.m, ameliore.m, frac.m, DessineLune.m et DemoCalLune.m.