Résumé : le problème de la représentation plane de la Terre se pose depuis les anciens Grecs, au départ pour des problèmes de navigation. Et à juste titre : il est en effet impossible d’aplatir une sphère sans déchirure ni déformation, autrement dit il n’existe aucune application d’une sphère sur le plan conservant les distances, même localement, ni même aucun homéomorphisme entre une sphère complète et un plan. Plusieurs projections peuvent être imaginées pour donner une représentation la plus fidèle de notre bonne vieille Terre.
Mots-clés : projection, sphère, homéomorphisme, perspective, dérivation.
L’exercice s’inspire de l’article Les projections cartographiques de Yann Ollivier, Quadrature, No 26, 1996.
L’auteur de l’article suppose une Terre sphérique (ce qui est tout aussi intéressant qu’un ellipsoïde ou un géoïde). On repérera un point par sa longitude φ et sa latitude θ.
On peut classer les projections selon les propriétés géométriques des parallèles et des méridiens. Une projection est dite :
On voit qu’une projection cylindrique s’apparente à une projection géométrique de la sphère sur un cylindre tangent à l’équateur qui est ensuite développé :
Une projection conique ou tronconique est comparable à une projection sur un cône dont l’axe passe par les pôles :
Une projection azimutale peut être rapprochée d’une projection sur un plan tangent au pôle (vue de dessous) :
Une projection obtenue par une véritable projection géométrique de la sphère à partir d’un centre sur une surface quelconque qui sera ensuite développée est dite perspective.
Mais les projections sont surtout classées selon les propriétés qu’elles conservent (pour les optimistes) ou le type de déformations qu’elles induisent (pour les pessimistes) :
Les projections
Les autres projections sont dites aphylactiques.
Hors de cette classification, une projection azimutale conserve les angles dont le sommet est le centre de la projection (les azimuts) et les projections orthodromiques conservent les géodésiques.
Le but du problème est de représenter la Terre suivant chacune des classifications données.
Il existe des conditions simples pour juger de l’équivalence ou de la conformité
d’une projection. On notera M le point de la sphère (de rayon pris égal à 1) de
longitude φ et de latitude θ, N son projeté de coordonnées x et y dans un repère
orthonormé (0,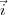 ,
,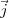 ) , avecx = ρcosγ et y = ρsinγ.
) , avecx = ρcosγ et y = ρsinγ.
L’aire d’un petit élément de surface de la sphère, d’étendue dφ en longitude et dθ en latitude, est
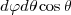
L’aire orientée de l’élément correspondant sur la carte est :
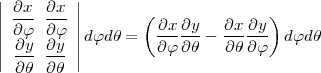
Si cette quantité est positive, on obtient une image directe de la région considérée, sinon on obtient une image retournée. L’échelle locale, pour les aires, d’une projection est donc définie comme
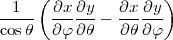
Pour une projection équivalente, cette quantité vaut 1, on en déduit :
Condition 1 : une projection est équivalente si et seulement si en tout point
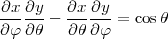
soit
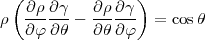
De la même manière, on définit l’échelle locale sur les méridiens par
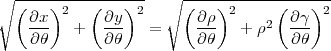
et sur les parallèles par
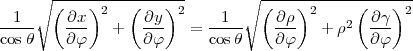
Une projection sera conforme si et seulement si elle est localement assimilable à une similitude, autrement dit si le quadrilatère représentant un petit rectangle dφdθ de la sphère est lui-même un rectangle et que les échelles des méridiens et des parallèles sont localement égales. On en déduit :
Condition 2 : une projection est conforme si et seulement si en tout point
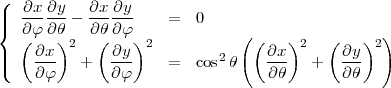
Pour avoir ceci en coordonnées polaires, il suffit de remplacer les termes en ∂x et ceux en ∂y par ρ∂θ.
Enfin, pour les projections équidistantes, l’échelle sur les méridiens vaut 1, ce qui donne :
Condition 3 : une projection est équidistante si et seulement si en tout point
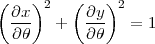
On peut appliquer ces résultats pour retrouver les projections couramment utilisées. On étudiera dans chaque catégorie principale (cylindrique, azimutale, tronconique) les projections perspectives, équidistantes, équivalentes, conformes.
Pour les projections cylindriques, on considérera un cylindre tangent à l’équateur, un cylindre sécant ou extérieur n’introduisant qu’un facteur d’échelle.
D’abord, la projection cylindrique perspective. On considérera que le point à partir duquel s’effectue la projection est le centre de la sphère, et que le cylindre est tangent à l’équateur. On trouve alors x = φ et y = tanθ, en prenant un repère convenable. Cette projection, contrairement à ce qui traîne dans de nombreux manuels de géographie, est différente de Mercator. Elle déforme énormément et n’est jamais utilisée.
La projection cylindrique équidistante, comme toute projection cylindrique, s’écrit dans un repère convenable x = φ et y = f(θ) avec f(0) = 0. Pour obtenir l’équidistance, portons ceci dans l’équation donnée sous la condition 3. On obtient (f′(θ))2 = 1, soit, puisque f(0) = 0, f(θ) = ±θ. Pour avoir une carte non retournée, on prend bien sûr f(θ) = θ pour avoir une échelle des aires positive. Finalement x = φ, y = θ : on obtient la projection dite quadratique, ou des cartes plates carrées, la plus simple qui soit.
La projection cylindrique équidistante est de la même forme. Pour obtenir l’équivalence, x et y doivent vérifier la condition no 1 qui s’écrit alors f′(θ) = cosθ, d’où f(θ) = sinθ. On obtient donc x = φ et y = sinθ : c’est la projection cylindrique de Lambert (à ne pas confondre avec les nombreuses autres projections portant ce nom) ou isocylindrique. Elle s’obtient géométriquement par projection orthogonale de la sphère sur un cylindre tangent à l’équateur.
Enfin, la projection cylindrique conforme. Toutes les projections cylindriques vérifient la première condition énoncé sous 2. La deuxième condition s’écrit f′(θ) = 1∕cosθ. On vérifie que (Formulaires et tables de la CRM, page 77)
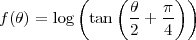
est la primitive de la fonction. Cette quantité est appelée « variable de Mercator » ou « latitude croissante ». Du fait de la propriété mentionnée ci-dessus, elle intervient directement dans beaucoup de projections conformes. La projection de Mercator ainsi définie est conforme mais exagère beaucoup les surfaces proches des régions polaires : à la latitude 45∘ l’échelle des aires est déjà 2.
Dans ce qui précède on a toujours supposé que l’échelle était conservée sur l’équateur. On peut, par une application affine, rendre un autre parallèle de vraie longueur et même le rendre automécoïque, c’est-à,dire supprimer toute déformation à son niveau, de manière à conserver les autres propriétés de la projection (équidistance, équivalence, conformité). Ceci signifie que la carte est conforme le long de ce parallèle et que les deux échelles locales selon les parallèles et les méridiens valent 1.
Si la projection cylindrique s’écrit x = φ et y = f(θ), et si on veut conserver le parallèle de latitude θ0, il suffit de prendre
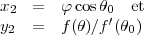
La projection quadratique devient ainsi la projection « des cartes plates parallélogrammatiques ». Pour la projection de Mercator, ceci est une simple homothétie (cette projection est déjà conforme partout).
A partir de la projection cylindrique de Lambert, on peut obtenir, en particulier, la fameuse projection de Peters, dont il convient de dénoncer l’hypocrisie : elle se présente en alternative de la projection de Mercator, dans laquelle les pays en voie de développement, de faible latitude, sont plus petits que les autres ; la projection de Peters, elle, conserve bien les surfaces, mais on a choisi θ0 de manière à ne pas déformer les pays développés, ce qui a pour conséquence, naturellement, de déformer considérablement les P.V.D., et ceci est souvent présenté comme une fatalité, le prix à payer pour obtenir l’équivalence !
Avant de passer aux projections azimutales, considérons, pour le plaisir, le problème suivant : trouver une projection méricylindrique équivalente telle que les parallèles soient régulièrement espacés. On a ici, toujours en posant l’équidistance sur l’équateur, x = φf(θ) et y = g(θ) avec f(0) = 1, g′(θ) = Cste et g(0) = 0. On doit, en tout point, avoir f(θ)g′(θ) = cos θ, d’où une famille de projections x = kφcosθ et y = θ∕k, et l’échelle sur le méridien central 1∕k, ce qui incite à prendre k = 1, projection qui sera conforme sur l’équateur, qui représentera toutes les parallèles par leur véritable longueur et qui sera équidistante sur le méridien central. Cette projection est appelée sinusoïdale, ou de Sanson, ou de Flamsteed.
Les projections azimutales sont de la forme γ = φ, ρ = g(θ), avec g(π∕2) = 0, ou plus simplement, en posant z = π∕2 - θ (z est la colatitude de M et simplifie les calculs), γ = φ, ρ = f(z) avec f(0) = 0.
Il existe une infinité de projections azimutales perspectives (comme de projections cylindriques perspectives). On n’étudiera donc que deux cas : le point de vue est soit au centre de la sphère, soit à l’infini. Pour les mêmes raisons que pour les projections cylindriques on considérera uniquement des projections sur un plan tangent, de manière à ne pas avoir de déformation au voisinage du point central (donc f′(0) = 0).
Voici une figure pour le premier cas où ρ = tanz. Ceci est la projection gnomonique ou (centrale). Elle ne peut représenter qu’un hémisphère et déforme beaucoup, mais elle est orthodromique : en effet le plan de tout grand cercle de la sphère passe par le centre de projection, et donc tout grand cercle sera représenté par une droite, et réciproquement.
Dans le second cas, on obtient une projection orthogonale, appelée projection orthographique où ρ = sinz. Cette projection ne peut, représenter qu’un hémisphère et aplatit considérablement les zones proches de l’équateur, mais les parallèles ont leur vraie grandeur, et surtout elle correspond à la vision de la Terre pour un observateur placé dans l’espace, et est donc visuellement satisfaisante.
Pour la projection azimutale équidistante, dite de Guillaume Postel, on trouve simplement f(z) = z (au signe près, qui n’est qu’une rotation).
Pour la projection azimutale équivalente, dite azimutale de Lambert, la condition 1 s’écrit
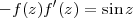
d’où
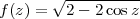
(au signe près) : le rayon est égal à la longueur de la corde joignant A, point de tangence, à M.
Pour la projection azimutale conforme, la première équation de la condition no 2 est vérifiée par toutes les projections azimutales (et même coniques). La deuxième s’écrit
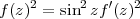
d’où on tire
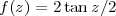
Ceci est la projection stéréographique et elle correspond en fait à une projection perspective dont le point de vue serait diamétralement opposé au point de tangence.
Les projections tronconiques (souvent simplement appelées coniques) sont de la forme γ = nφ et ρ = f(θ). Du fait qu’on n’a pas forcément f(π∕2) = 0 et que n est paramétrable, on peut fixer deux conditions supplémentaires : généralement on impose à deux parallèles d’être automécoïques. Cette classe de projection est très intéressante car elle permet d’obtenir les projections cylindriques et azimutales comme cas limite (un cône dont le sommet est à l’infini ou au contraire sur la sphère), et offre donc une plus grande variété. Cependant, ceci est rarement reconnu car on n’utilise, à tort, que l’aspect direct des projections coniques.
La condition de rendre un parallèle θ0 automécoïque s’écrit
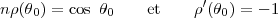
En partant de deux parallèles automécoïques (que nous noterons θ1 et θ2), et en raisonnant comme précédemment, on trouve n et ρ. Les calculs sont parfois longs mais restent simples, et on peut donc se contenter d’énoncer les résultats. On peut aussi imposer qu’autour d’un parallèle, l’erreur soit seulement du second ordre, ce qui revient à faire tendre θ1 vers θ2 dans les expressions pour 2 parallèles distinctes. Une façon équivalente d’obtenir ce cas particulier consiste à poser
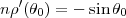
ce qui avec ρ′(θ0) = -1 aboutit à n = sin(θ0). Dans les paragraphes qui suivent nous donnons entre crochets [ ] le cas particulier d’un parallèle de second ordre.
Pour la projection conique équidistante ou projection de Delisle, on trouve
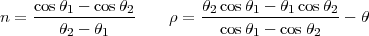
![[n → sinθ0 ρ → cotanθ0 + θ0 - θ]](am272x.png)
Pour la projection conique équivalente (projection d’Albers), on trouve
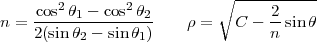
avec
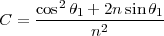
![[ 1+ sin2θ0]
n → sinθ0 C → ----2-----
sin θ0](am275x.png)
(comparer avec la projection azimutale de Lambert quand θ1 = θ2 = π∕2).
Enfin, pour la projection conique conforme ou projection conique de Lambert on a
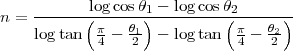
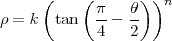
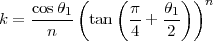
La solution actuellement proposée est donnée par les fichiers MatLab : projo.m.