Chapitre 51
Une forêt fractale

Résumé : en partant de la relation d’Euler et en manipulant des nombres complexes, on peut produire des images fractales très belles qui rappellent des forêts.

Mots-clés : nombre complexe, relation d’Euler, fractal.

Enoncé

L’exercice s’inspire des articles Complex power iteration et A beautiful new playground de Greg Parker, Steve Abbot et Steve Roberts, The Mathematical Gazette, No 492 et No 493, 1997-98.

Quelles sont les constantes mathématiques les plus connues ? De manière générale, on répondra π, e, i, 0 et 1. Léonard Euler a énoncé une relation, désormais très célèbre, entre ces cinq constantes :

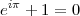
Une autre propriété extraordinaire de cette relation, moins bien connue mais de conséquence égale, réside dans le fait qu’en élevant un nombre complexe à une puissance complexe, on peut obtenir un résultat réel.

Comme e^ix = cosx + isinx, il est possible de vérifier que

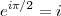
et, en élevant les deux côtés de l’équation à la puissance i, on obtient :

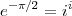
Evidemment, e^-π∕2 est un nombre réel égal à iⁱ. En calculant, on obtient :

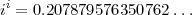
Que se passe-t-il lorsque l’on repète ce processus ? Ou encore, quelle est la limite de la suite {T_n} définie par T₁ = i, T_n+1 = i^T_n ?

Pour construire l’image fractale proposée par les auteurs, on définira la suite suivante :

On peut généraliser et prendre la routine d’itération suivante :

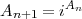
où A₀ = i. Comme la suite converge vers une limite, on peut écrire :

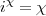
et si χ = x + iy, on trouve les équations suivantes :

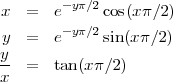
N’importe quel nombre complexe peut être utilisé dans la routine d’itération ci-dessus en remplaçant i et A₀ par le nombre complexe considéré. On trouvera alors dans de nombreux cas la limite χ. Ce n’est pas le cas pour toutes les valeurs et la vitesse de convergence varie d’un nombre à l’autre.

Ces résultats expérimentaux suggèrent une méthode pour produire un nouveau fractal : pour chaque nombre complexe choisi dans un domaine précis, on produit l’itération en remplaçant A₀ par le nombre complexe. On compte le nombre d’itérations requises pour atteindre χ (avec une précision donnée, par exemple, 10^-5) ou non. On attribue une couleur à ce nombre (en on utilise le noir ou le blanc pour la suite qui ne converge pas après une limite donnée).

Si tout se passe bien, et si l’on dispose d’un ordinateur et d’un logiciel de mathématiques puissant, on obtient des images comme celle-ci :

Le but de l’exercice consiste à représenter des forêts fractales sur le modèle ci-dessus.

Indications

Les indications données dans le paragraphe énoncé devraient suffire.

Il faut toutefois rester attentif à la façon de calculer la puissance complexe d’un nombre complexe. On utilise en effet la fonction complexe du logarithme qui est multivaluée. En fait, iⁱ = eⁱ = e^{-(π∕2+2nπ)} où n peut être n’importe quel entier.

Toutefois, e^-π∕2 est la valeur principale de iⁱ.

Solutions

La solution actuellement proposée est donnée par les fichiers MatLab : puissi.m, demoPuissi.m, fracPuiss.m et demoFrac.m.