Résumé : les anneaux de Borromée ne sont pas reliés deux à deux, et pourtant le groupe ainsi formé est indissociable. Si l’on sectionne l’un des trois anneaux, on obtient trois anneaux séparés.
Mots-clés : topologie, nœud, courbure.
L’exercice s’inspire du livre La Spirale de l’escargot, contes mathématiques de Armand Herscovici, Seuil, 2000.
Un chapitre du livre décrit la véritable histoire de Thésée et du Minotaure :
« Thésée commençait à en avoir par-dessus la tête. Voilà des heures qu’il essayait en vain de défaire ce nœud stupide et colossal. S’il tirait sur un brin, pensant ainsi dénouer une boucle, un autre nœud encore plus gros apparaissait aussitôt, généré par un étranglement inattendu. Si, au contraire, il donnait du mou, il ne faisait que donner naissance à une boucle supplémentaire.
Finalement, c’était sa propre tension qui montait. En fait d’étranglement, c’est à celui d’Ariane qu’il rêvait, au fur et à mesure que son énervement augmentait ; la rage le gagnant, il lui venait l’envie de jeter à terre cet amas ridicule de ficelles emmêlées, pour le piétiner jusqu’à l’écrasement définitif.
Car enfin, elle ne faisait que des bêtises, cette mijaurée d’Ariane. Tout d’abord, au lieu de lui préparer son épée en acier inoxydable, elle s’était trompée, et lui avait donné l’épée de fer, certes plus resplendissante, avec sa poignée incrustée de pierres précieuses, mais qui commençait à rouiller dans l’atmosphère humide et salée du Labyrinthe. D’ailleurs s’était-elle réellement trompée, et n’était-ce pas pour un stupide motif esthétique qu’elle avait interverti les armes ? Et maintenant, il devait combattre ce gros bœuf de Minotaure à la force des ses poings nus !
Mais, surtout, c’était l’affaire du fil qui le mettait hors de lui. Comment imaginer un seul instant pouvoir retrouver son chemin par ce moyen ridicule, alors que c’était ce vieux croûton de Dédale qui avait imaginé le plan biscornu du Labyrinthe. Il était évident que l’esprit retors du machiavélique architecte avait conçu la construction de telle sorte que l’on soit systématiquement contraint de passer plusieurs fois au même endroit. Le fil de cette pimbêche d’Ariane ne pouvait se croiser avec lui-même à de multiples reprises, s’entremêler, et se transformer en un paquet de nœuds inextricables. C’était exactement ce qui s’était produit.
Maintenant, il était là, à perdre son temps comme un imbécile, sentant une invincible exaspération l’envahir.
Sa décision était prise. Dès que cette affaire avec ce veau de Minotaure serait réglée, il emmènerait cette pécore d’Ariane (qui d’ailleurs, il s’en rendait compte maintenant, ressemblait de plus en plus à sa mère, Pasiphaé) sur l’île de Naxos, et s’arrangerait pour l’y laisser en compagnie d’un paysan du coin, ou de quelque autre compagnon.
Un nœud imprévu étant apparu à la suite d’une manipulation maladroite, sa fureur atteint un paroxysme. Il poussa un hurlement rageur et jeta l’amas de nœuds à terre. Il s’apprêtait à le hacher menu avec son épée rouillée, lorsqu’il sentit que quelqu’un lui tapotait discrètement l’épaule. Il se retourna, et se retrouva face à face avec le Minotaure.
Lorsqu’il avait débarqué en Crète, où il venait pour occire le Minotaure, Thésée était allé voir un philosophe local qu’on lui avait chaudement recommandé, afin de s’informer sur le monstre. Ce phare de la pensée crétoise n’avait pas tari, décrivant avec force qualificatifs le caractère sanguinaire, cruel, féroce, de la terrible créature. Puis, en bon philosophe grec qu’il était, il avait ajouté en riant, faisant allusion à un trait bien connu des méridionaux : « Mais rassure-toi, Thésée, tous les Crétois sont des menteurs. » Peu de temps après cette déclaration, Thésée avait été saisi d’une violente migraine : « Si tous les Crétois sont des menteurs, ce philosophe, crétois lui-même, ment ; notamment lorsqu’il prétend que les Crétois sont des menteurs. », s’était-il dit. « Par conséquent, avait-il conclu, les Crétois ne sont pas des menteurs. Mon philosophe ne ment donc pas, puisqu’il est crétois, en particulier lorsqu’il indique que les Crétois sont menteurs ! Les Crétois sont donc des menteurs et mon philosophe aussi. Finalement, s’il ment, il ne ment pas, et s’il ne ment pas, il ment. » La logique se mordait la queue, et le paradoxe était inventé.
Mais trêve de balivernes, une chose ne pouvait prêter à contestation : le Minotaure qu’il avait maintenant en face de lui était terrifiant.
(...) –Mon cher Thésée, répondit le Minotaure, tu n’imagines tout de même pas que je reste ici à me morfondre, sans avoir développé une quelconque activité qui puisse m’occuper l’esprit. En fait, j’ai considérablement travaillé sur l’organisation de ce labyrinthe, j’en ai déduit de nombreuses lois et règles générales, et je suis devenu le meilleur spécialiste mondial de la topologie. Je suis d’ailleurs universellement connu dans le cercle restreint des topologistes, je suis l’auteur de nombreuses publications, et je postule au prix Nobel de topologie.
–Mais la topologie, c’est quoi ?, demanda Thésée qui excellait plutôt dans les disciplines physiques. »
Sans répondre, le Minotaure se leva. Il se dirigea vers le fil d’Ariane transformé en tas de nœuds, posa un pied sur un brin, le second sur un autre brin, empoigna fermement des deux mains une petite boucle qu’il maintient ouverte, y glissa l’une de ses grandes cornes, et d’une torsion rapide de son cou puissant tira sur l’ensemble. Comme par miracle, l’amas sembla fondre instantanément, les nœuds croisés et mélangés disparurent comme par enchantement, et l’ensemble revint à sa structure filiforme originelle.
« Mon cher Thésée, dit simplement le Minotaure, tu viens d’assister à une application pratique des théories de la topologie. »
Le pauvre Thésée, qui avait sans succès sué sang et eau pendant des heures pour essayer d’arriver à ce résultat, en resta coi d’étonnement ; son respect pour le Minotaure s’en trouva accru dans des proportions considérables.
« Mon brave Thésée, reprit le Minotaure, je pourrais également répondre à ta question d’une autre manière, en précisant – et ce serait l’exacte vérité – que la topologie est la branche des mathématiques qui s’intéresse à l’étude des déformations continues en géométrie, et aux rapports entre la théorie des surfaces et l’analyse mathématique. Si je ne craignais d’attrister encore ton sombre regard de héros grec, je n’hésiterais pas à évoquer les homéomorphismes, les plongements et isotopies, les recollements de topologies, les applications homotopes, les ensembles simpliciaux de polyèdres, les homologies singulières, les espaces fibrés, et bien entendu le cobordisme (car la transversalité intervient constamment en topologie différentielle).
(...) – Mais on pourrait aller plus loin, et étudier, comme le font les topologistes, des combinaisons de nœuds. Je ne t’en montrerai qu’un exemple, mais sa beauté te fera peut-être regretter que l’on aille plus avant dans cette étude. Il s’agit des anneaux de Borromée.
Ce sont trois anneaux, donc trois nœuds triviaux, connectés comme ci-dessous. Aucun des couples d’anneaux (c’est-à-dire les anneaux pris deux à deux) ne s’interpénètrent : les anneaux de chaque couple sont indépendants l’un de l’autre. C’est uniquement l’ensemble des trois qui est indissociable. Mais il suffit de sectionner l’un des trois pour que l’ensemble se disjoigne. N’est-ce-pas étonnant ? Et maintenant Thésée, que penses-tu de la théorie des nœuds ? »
On imagine facilement la symbolique de collaboration qu’ils peuvent représenter. Des sociétés commerciales l’ont utilisé comme logo, des campus universitaires les font trôner à leur entrée.
Les anneaux de Borromée tirent leur nom d’une célèbre famille de princes italiens de la Renaissance, les Borromée, qui les adoptèrent comme symbole héraldique. Ils sont gravés dans la pierre de leur château, sur une île du lac Majeur, dans le nord de l’Italie.
On les retrouve également sur des pierres sculptées à Gotland, une île de la mer Baltique au large des côtes sud-est de la Suède. Ils datent du IXe siècle environ. On pense qu’ils correspondent à des légendes découlant de mythes nordiques. Par ailleurs, les peuples du nord de la Scandinavie connaissent une représentation des anneaux de Borromée en forme de triangles sous le nom de « triangle d’Odin », « nœud du tué ». Le symbole était également gravé sur les montants des lits utilisés lors des funérailles en mer.
L’aspect paradoxal de ces anneaux, lorsqu’on les regarde en plan, c’est-à-dire dessinés sur une feuille de papier, vient de ce qu’en réalité ils sont forcément courbés dans l’espace ; et cette courbure n’apparaît pas dans la vue projetée. La nécessité de la courbure a été démontrée mathématiquement (bel exemple d’une évidence visuelle, pourtant très difficile à démontrer). Le dessin ci-dessous fait apparaître l’indispensable courbure.
Pour résoudre ce problème, il suffit de représenter trois cercles dans l’espace. Ces trois cercles ont des centres placés sur les sommets d’un triangle équilatéral.
Pour représenter les anneaux, il faut imaginer une hauteur pour chaque cercle qui varie selon une période de trois oscillations.
Quelques informations précises : pour un cercle de rayon 1, on peut prendre un
décalage de 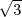 ∕3 ; pour les oscillations, on peut prendre une courbe de la forme :
cos(3t)∕3.
∕3 ; pour les oscillations, on peut prendre une courbe de la forme :
cos(3t)∕3.
La solution actuellement proposée est donnée par les fichiers MatLab : borromee.m et ver3h.m.