Résumé : Parmi les formes de la vie et les forces qui les modèlent, on peut citer : l’enroulement des cornes des défenses, la structure des rayons de miel et des toiles d’araignée, l’arrangement des coquilles et des ailes de libellules, entre autres merveilles. Dans cet exercice on s’intéresse particulièrement aux coquillages et à leurs modèles.
Mots-clés : spirale équiangle, progression géométrique, progression arithmétique, hélico-spirale.
L’exercice s’inspire du livre Forme et croissance de D’Arcy Thompson, Seuil, 1994 et The Algorithmic Beauty of Sea Shells de Hans Meinhardt, Springer, 1995.
Dans la préface du livre Forme et croissance, Stephen Jay Gould décrit ce chef d’œuvre : D’Arcy Wentwoth Thompson (1860-1948), professeur de zoologie à l’université de Saint Andrews en Ecosse et peut-être l’esprit le plus universel de ce siècle, ne fut pas homo unius libri (l’homme d’un seul livre), loin s’en faut. Auteur d’un commentaire en deux volumes sur les oiseaux et les poissons mentionnés dans les textes grecs classiques, on lui doit également la traduction de référence de l’Historia animalium d’Aristote ; en outre, nous savons qu’il analysa, des années durant, les statistiques des pêcheries d’Ecosse et qu’il rédigea, pour la série Cambridge Natural History, l’article sur les pyconogonidés (un groupe d’arthropodes mineur, mais fascinant). Cependant, cette réputation durable, et qui ne cesse en fait de croître au fil des ans, il la doit à un ouvrage magistral (et très long) qui, plutôt qu’une étape de sa propre évolution, est l’aboutissement du travail de toute une vie : On Growth and Form (1re éd., 1917 ; 2e éd. 1942)...
Si l’on en croit une légende qui aurait pu être vraie, D’Arcy Thompson se vit offrir le choix d’une chaire de professeur dans trois disciplines sans lien apparent : lettres classiques, mathématiques et zoologie. Ce qui est remarquable dans On Growth and Form c’est que précisément ces trois disciplines y sont profondément intégrées, sans qu’on puisse à aucun moment soupçonner l’auteur d’ostentation.
Dans ce superbe ouvrage, on y trouve un chapitre sur la coquille des mollusques : « il y a plus de cent ans le chanoine Moseley nous a donné une interprétation mathématique simple de la forme en spirale des coquilles univalves, et son article reste un grand classique de l’histoire naturelle. Mais bien d’autres — certains avant lui, certains parfois longtemps après — avaient étudié le problème et avaient entrevu cette même simplicité dans la forme et la structure des coquilles. Aux environs de 1818, Reinecke avait déclaré que la coquille de Nautillus correspondait à une figure géométrique bien précise, dont les différentes chambres se succédaient selon un rapport constant, selon une proportion continue ; Leopold von Buch puis d’autres après lui se rallièrent à cette idée, et poursuivirent même son développement. »
« Bien auparavant, Swammerdam avait saisi, avec une perspicacité encore plus grande encore, où se trouvait la racine du problème ; en s’appuyant sur quelques exemples variés tels que ceux de Helix ou de Spirula, il montra que la forme des coquilles, comme celle de toutes les autres coquilles en spirale, relevait d’un même type, celui d’une simple tubulure courbée de diverses manières selon des lois mathématiques bien précises ; et, quels que soient les ornements, épines, tubérosités ou autres bandes colorées surajoutées à ces coquilles, il s’agissait toujours en fait du même type de forme, les différences propres à chaque espèce étant d’origine géométrique. »
Nous pouvons nous représenter comme suit la surface de toute coquille, qu’elle soit discoïde ou turbinée (en cornet) : c’est la surface engendrée par la révolution, autour d’un axe fixe, d’une courbe fermée dont les dimensions augmentent continûment, mais qui reste en permanence semblable à elle-même sur le plan géométrique. De plus, l’échelle de la figure croît selon un progression géométrique, alors que l’angle de rotation augmente suivant une progression arithmétique, et le centre de similitude est fixe. Dés lors, la courbe dessinée dans l’espace par les points correspondants de la courbe génératrice est, elle, dans tous les cas une spirale équiangle. Pour les coquilles discoïdes telles que celles des nautiles, des argonautes ou des ammonites, la figure génératrice est en révolution dans un plan perpendiculaire à l’axe. Chez les coquilles turbinées, cette figure suit un trajet incliné par rapport à l’axe de révolution, et la courbe engendrée dans l’espace par un point quelconque forme un angle constant avec l’axe du cône, qui enveloppe le tout et adopte dès lors aussi bien les caractéristiques d’une hélice que celles d’une spirale logarithmique ; il s’agit d’une hélico-spirale.
Les coquilles de l’escargot, du bigorneau et de tous les gastéropodes courants typiques appartiennent à cette catégorie de coquilles turbinées ou hélico-spirales.
Toute section de la coquille, parallèle, perpendiculaire ou inclinée d’un angle quelconque par rapport à l’axe, peut constituer la figure génératrice. Le plus souvent, on assimile celle-ci au contour de l’ouverture de la coquille ; il s’agit alors parfois d’une courbe plane, de forme simple, mais, le plus souvent, elle adopte une forme plus complexe dont le contour n’est pas toujours situé dans un seul et même plan : il est alors possible de lui substituer un « tracé », dans un plan formant un angle bien défini avec la direction de la croissance, par exemple la forme qui apparaît dans une section transversale parallèle à l’axe de la coquille hélicoïdale. La courbe génératrice adopte des formes très variées. Elle est circulaire chez Scalaria, Cyclostoma et Spirula ; on peut la considérer comme une portion de cercle chez Nautica ou Planorbis. Elle est triangulaire chez Conus ou Tchatcheria, et rhomboïde chez Solarium ou Potamides. Très souvent la courbe génératrice adopte plus ou moins la forme d’une ellipse : chez Oliva et Cypraea, le grand axe de l’ellipse est parallèle à celui de la coquille ; chez de nombreux troches, il est loin d’être perpendiculaire à cet axe, et dans de nombreux cas bien documentés, tels que Stomatella, Lamellaria, Sigaretus haliotoides et Haliotis, le grand axe de l’ellipse est oblique par rapport à celui de la coquille. Cette courbe génératrice devient presque une demi-ellipse chez Nautilius pompilius et un peu plus d’une demi-ellipse chez N. umbilicatus, le grand axe étant dans les deux cas perpendiculaires à l’axe de la coquille. La forme de cette courbe ne se prête que rarement à une expression mathématique simple, sauf quand il s’agit d’un vrai cercle ou d’une vraie ellipse ; il existe cependant une exception à cette règle chez certaines ammonites, celles du groupe de « Cordati », où la courbe génératrice correspond presque exactement à une cardioïde d’équation r = a(1 + cosθ).
Lorsque deux courbes génératrices des spires successives se coupent, leur ligne d’intersection forme l’inévitable hélico-spirale, ou courbe loxodromique que les conchyliophilistes appellent la suture.
La croissance de la courbe génératrice est tantôt lente tantôt rapide ; son facteur de croissance est très lent chez Dentalium ou Turritella, très rapide chez Nerita, Pileopsis, Heliotis ou la patelle. Parfois, comme chez Nautilus, le plan de la courbe contient l’axe de la coquille ; parfois, comme chez la plupart des gastéropodes, ce plan est parallèle à l’axe.
L’apparence générale du coquillage est déterminée — hormis la forme de sa courbe génératrice — par la valeur de trois angles, ceux-ci dépendant à leur tour des rapports de certaines vitesses de croissance. Ces angles sont :
L’angle spiral (α) est très petit chez une patelle, où on lui attribue généralement une valeur de 0∘ ; mais, bien entendu la valeur de cet angle n’est pas nulle, même si la coquille tubulaire excessivement courte lui donne cette apparence. Chez Dentalium, la valeur de cet angle est encore assez faible, mais suffisante cependant pour donner l’apparence d’une courbe régulière ; cette valeur approche sans doute 30 ou 40∘. Chez Haliotis, elles est comprise entre 70 et 75∘ ; chez Nautilus, elle est voisine de 80∘ ; et elle se situe entre 80 et 85∘, ou même plus, chez la majorité des gastéropodes.
L’angle α n’est pas toujours — ni rigoureusement — constant. Chez certaines ammonites, il augmente avec l’âge, induisant un rapprochement des spires ; chez d’autres, au contraire, il diminue rapidement et devient même nul, provoquant un étalement de la coquille enroulée à l’origine.
Il est très courant d’observer une variation de β en fonction de l’âge du coquillage, mais il nous faut rarement distinguer ou dissocier cette altération de celle de l’angle α.
L’angle de retard (γ) est très faible chez Dentalium et Patella ; il est très important chez Haliotis ; et devient infini chez Argonauta et Cypraea. D’autres facteurs sont liés au problème de l’angle de retard, telles les diverses possibilités de contact ou de séparation, plus ou moins prononcées, entre les spires adjacentes d’une coquille discoïde, ou entre les spires adjacentes et opposées d’une coquille turbinée.
Le but du problème consiste à modéliser la géométrie d’une coquille de mollusque à l’aide d’un ordinateur. Le deuxième ouvrage mentionné, The Algorithmic Beauty of Sea Shells est également une petite merveille : il illustre plus particulièrement la croissance des motifs qui apparaissent sur les coquillages.
La construction des modèles dérivés de celui décrit par D’Arcy Thompson peut être schématisée comme suit :
La modélisation de la surface d’une coquille de mollusque débute par la construction d’une hélico-spirale H.
En coordonnées cylindriques, la surface peut être décrite comme suit :
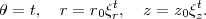
Le paramètre t est compris entre 0 au sommet de la coquille et tmax à l’ouverture. Les deux premières équations représentent une spirale logarithmique dans le plan z = 0. La troisième équation étire la spirale le long de l’axe des z, permettant ainsi de créer une hélice.
Les distances r et z sont des fonctions exponentielles de t, et habituellement ont la même base ξr = ξz = ξ. Ceci a pour résultat que l’hélico-spirale est autosimilaire, avec un centre de symétrie situé à l’origine du repère xyz. Si les valeurs θ0, r0 et z0 sont données, la suite des points le long de l’hélico-spirale est donnée par la formule :
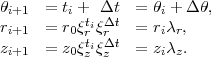
Lorsque l’angle de rotation θ augmente selon un progression arithmétique de pas Δt, le rayon r varie selon un progression géométrique de facteur λr = ξrΔt, et le déplacement vertical z selon un progression géométrique de facteur λz = ξzΔt. Dans de nombreux coquillages, les paramètres λr et λz sont identiques.
La surface du coquillage est déterminée par la courbe génératrice C, tournant autour de l’hélico-spirale H. La taille de la courbe C augmente en tournant autour de l’axe du coquillage.
La courbe génératrice C est spécifiée en coordonnées locales uvw. Soit un
point H(t) de l’hélico-spirale, la courbe C est d’abord mise à l’échelle par un
facteur ξct par rapport à l’origine O du système puis, tournée et translatée de
telle sorte que O coïncide avec H(t). Les axes uvw sont utilisés pour
orienter la courbe génératrice dans l’espace. L’approche la plus simple
consiste à tourner le système uvw de sorte que les axes v et u deviennent,
respectivement parallèle et perpendiculaire à l’axe du coquillage z. Si la courbe
génératrice se trouve dans le plan uv, l’ouverture du coquillage et les traces de
croissance seront parallèles à l’axe du coquillage. En revanche, plusieurs
coquillages disposent de traces de croissances qui se trouvent dans des
plans perpendiculaires à l’hélico-spirale H. Cet effet peut être réalisé en
orientant l’axe w le long du vecteur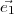 
, tangent à l’hélico-spirale au point
H(t). La courbe est fixée dans l’espace en alignant l’axe u avec le vecteur
normal 
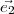à H. Les vecteurs unitaires 
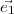et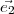 
peuvent être calculés comme
suit :
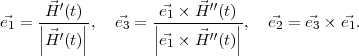
Les symboles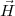 
′(t) et 
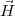′′(t) décrivent les première et seconde dérivées du
vecteur position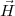 
(t). Les vecteurs 
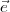2 et 
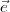3 définissent un système de
coordonnées orthonormé appelé cadre de Frenet.
La solution actuellement proposée est donnée par les fichiers MatLab : democoquillage.m, ver3.m et helico.m.