Résumé : heureux celui qui arrivera à remettre en place le puzzle intitulé Lucky 7. Ce jeu a un intérêt mathématique et informatique car il est possible de démontrer que, quelle que soit la configuration initiale, une solution existe.
Mots-clés : permutation, cycle.
L’exercice s’inspire du site Internet www.cut-the-knot.com de Alexander Bogomolny.
Alexander Bogomolny y décrit un jeu consistant à remettre des pions numérotés (de un à sept) en place après qu’ils aient été mélangés. Le puzzle se compose de plusieurs pions numérotés placés sur deux cercles qui se coupent. Il y a six pions de commande : les deux pions centraux (dont un ne porte pas de numéro) et les deux paires de pions situés de part et d’autre des pions centraux.
Dans le cas où il y a sept pions, les commandes sont assurées par le pion vide et les pions numérotés 1, 7, 3, 4 et 5. En agissant sur les pions du haut, on fait tourner les pions dans le sens horaire ; sur les pions du bas, dans le sens contraire des aiguilles d’une montre. Les pions à gauche font tourner le cercle de gauche ; les pions à droite, le cercle de droite, les pions du centre, font tourner les deux cercles à la fois. Le pion vide est sauté dans tous les cas.
Le but du problème est d’utiliser l’ordinateur pour simuler et représenter le jeu Lucky 7.
Avec 7 pions, le puzzle est soluble pour n’importe quelle configuration initiale. Formulé comme ceci, il s’agit d’un théorème. Pour le démontrer, Alexander Bogomolny propose la preuve suivante.
Soit a une rotation d’un cran dans le sens horaire du cercle de gauche et b, une rotation d’un cran dans le sens horaire du cercle de droite. Alors la suite de rotations
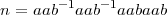
permute les pions 6 et 7 et aussi la paire 2 et 4. En autre terme, cette suite mène à la permutation n =(1)(2 4)(3)(5)(6 7).
D’autre part, pour la suite m = aabaabaabaabaab, on a m =(1 3)(2)(4) (5)(6)(7).
Soit c, la rotation des deux cercles dans le sens horaire, alors cmc-1 =(1) (2 4)(3)(5)(6)(7). Cela signifie que ncmc-1 =(1)(2)(3)(4)(5)(6 7).
On a ainsi trouvé une suite de rotations qui permutent deux pions adjacents (6 et 7). Ceci montre également que deux pions adjacents quelconques peuvent être permutés par une suite de rotations sans mélanger les autres. En effet, suivant k, la suite ckncmc-1c-k permute n’importe quelle paire de pions adjacents. Par exemple, si k = 1, les pions 1 et 7 permutent, si k = 2, les pions 1 et 2 permutent, etc.
Supposons maintenant que nous souhaitions permuter une paire quelconque de pions, A et B. Soit f une suite de rotations qui mène A en position 6 et B en position 7. On ne s’intéresse pas aux autres pions. Permutez les pions en position 6 et 7 puis, appliquez les rotations inverses de f mais à l’envers. Tous les pions retourneront dans leurs positions initiales mais, A et B auront été permutés.
Ainsi toutes les transpositions peuvent être produites par ces permutations de base. Ceci démontre le théorème puisque le pion 1 peut être permuté pour atteindre sa position initiale puis, le pion 2 et ainsi de suite. CQFD.
La solution actuellement proposée est donnée par les fichiers MatLab : lucky7.m.