Résumé : comment fabrique-t-on un labyrinthe de qualité ? Il doit avoir des propriétés intéressantes : chaque point dans le labyrinthe doit pouvoir être relié à un autre point et il ne doit y avoir qu’un chemin possible. Pour de grands labyrinthes, il est avantageux de faire appel à l’ordinateur : en définissant une structure de données intelligente, le problème peut être considérablement simplifié.
Mots-clés : liste, arbre, connectivité, acyclicité, structure de données, ensemble de Tarjan.
L’exercice s’inspire de la mythologie grecque et du site Internet lampwww. epfl.ch/courses/mecaphys01/projet/donnee.html.
Les labyrinthes ont toujours fasciné les hommes. La mythologie en a utilisé abondamment. Dédale a construit un labyrinthe célèbre en Crète.
(Lu sur Internet : perso.wanadoo.fr/spqr/mino_mytho.htm) Zeus enleva Europe, la fille du roi de Phénicie qui jouait avec ses amies sur la plage de Tyr. Pour séduire Europe, Zeus se transforma en un superbe taureau d’une blancheur incomparable et très doux. Europe caressa l’animal et s’assit sur son dos. Aussitôt le taureau l’emporta à travers les flots jusqu’en Crète où Zeus s’unit à Europe sous les platanes de Gortyne. Ils eurent trois enfants : Minos, Radhamante et Sarpédon.
Minos, roi réel ou mythe, a laissé l’image d’un roi juste. Il recevait les ordres de son père tous les neuf ans. Minos, après sa mort, devint l’un des juges des Enfers.
Pour prouver à ses frères que les dieux sont avec lui, Minos demande à Poséidon de faire sortir des flots de la mer un taureau blanc qu’il promet de lui sacrifier en retour. Minos ne respecta pas sa promesse et préféra garder ce taureau pour assurer la reproduction de ses troupeaux. Poséidon se vengea en inspirant à Pasiphaé, la femme de Minos, un amour pour le beau taureau.
Pour assouvir sa passion, Pasiphaé demanda à l’architecte athénien Dédale, exilé en Crète, de lui construire une vache en bois recouverte de cuir dans laquelle elle se glissa pour s’accoupler avec le taureau. De cette union contre nature naquit le Minotaure, monstre pourvu d’une tête de taureau sur un corps d’homme et qui se nourrissait de chair humaine. Minos ordonna à Dédale de construire le labyrinthe, enchevêtrement de salles et de couloirs où nul ne pouvait retrouver son chemin, pour y cacher le monstre et exigea après sa victoire sur les Athéniens que ceux-ci lui envoient tous les trois ans quatorze jeunes de la cité (sept garçons et sept filles) pour nourrir le monstre.
Thésée, prince athénien, se porta volontaire pour le sacrifice. Ariane, la fille de Minos et de Pasiphaé tomba amoureuse de Thésée en le voyant et résolut de le sauver : elle lui confia une pelote de laine pour qu’il marque son chemin dans le Labyrinthe. Thésée tua le Minotaure et s’enfuit avec Ariane et les autres jeunes Athéniens. Ingrat, Thésée abandonna Ariane sur une plage de Naxos. Pour se venger, Minos enferma Dédale et son fils Icare dans le Labyrinthe. Dédale fabriqua des ailes avec des plumes et de la cire pour s’échapper du Labyrinthe. Icare durant son vol s’approcha trop près du soleil et la cire de ses ailes fondit : il fut précipité dans la mer qui porte désormais son nom, la mer Icarienne. Minos poursuivit Dédale jusqu’en Sicile où il mourut ébouillanté dans une baignoire inventé par le génial Dédale.
Phèdre, la sœur d’Ariane épousa Thésée dont elle eut deux enfants. Phèdre s’éprit d’Hippolyte son beau-fils. Accusé par Phèdre, Hippolyte fut banni puis exécuté. Phèdre, éprise de remords, se pendit.
Les labyrinthes posent des problèmes informatiques intéressants : comment les fabriquer et comment en sortir. Dans cet exercice, on s’intéresse exclusivement à la fabrication des labyrinthes en respectant deux conditions :
En terme de théorie des graphes, la première condition porte le nom de connexité et la seconde d’acyclicité. L’une assure que le labyrinthe a toujours une solution quels que soient les points de départ et d’arrivée, l’autre que l’on ne peut pas tourner en rond indéfiniment. Tout le monde conviendra que ce sont là de bonnes propriétés pour un labyrinthe.
Le problème est particulièrement intéressant du point de vue des structures des données. En choisissant une bonne structure de données, la part réservée à l’algorithmique est plus simple à mettre en œuvre.
Le labyrinthe est formé de cellules carrées séparées par des murs qui peuvent être ouverts ou fermés. C’est-à-dire que l’on considère que deux cellules voisines sont toujours séparées par un mur, mais que le passage de l’une à l’autre n’est possible que si ce mur est ouvert (au lieu de murs ouverts ou fermés on pourrait aussi parler de portes fermées à clé ou non).
Un labyrinthe rectangulaire est constitué de cellules rangées en lignes et en colonnes, comme sur un échiquier. On appelle largeur et hauteur d’un labyrinthe respectivement le nombre de colonnes et de lignes de ce labyrinthe. Chaque cellule est identifiée par un nombre entier. Le labyrinthe est entouré d’une enceinte avec une ouverture à chaque extrémité. Enfin, deux cellules voisines sont toujours séparées par un mur, celui-ci pouvant être ouvert ou fermé. Parmi ces murs, on distingue les murs verticaux et les murs horizontaux.
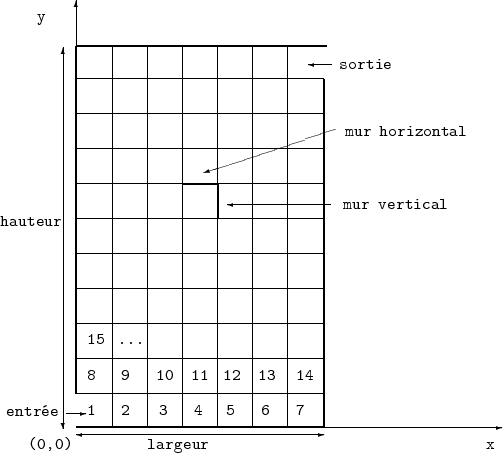
Il est conseillé de définir la structure de données suivante : un labyrinthe possède les attributs suivants : largeur, hauteur pour les dimensions du labyrinthe, nbre_murs pour le nombre de murs du labyrinthe et murs, un tableau qui contient la définition des murs.
Un mur possède les attributs suivants : cellule_1 et cellule_2 pour les indices des cellules séparées par le mur, ouvert de type booléen qui est vrai si le mur est ouvert et faux sinon, segment qui contient les coordonnées cartésiennes du mur.
On définit ensuite une procédure pour construire un labyrinthe : on commence par les murs verticaux puis les murs horizontaux. Une routine de dessin permet de représenter un labyrinthe quelconque ; au départ, tous les murs sont représentés et on obtient un échiquier.
Lors de l’ouverture des murs du labyrinthe, il est souvent nécessaire de savoir si deux cellules sont déjà reliées entre elles ou pas. Il est donc impératif de trouver une technique permettant d’effectuer cela de manière efficace. Une idée qui vient rapidement à l’esprit est de former des ensembles de cellules pour savoir lesquelles sont connectées entre elles. C’est-à-dire que dans un ensemble donné on place toutes les cellules qui sont reliées par un chemin.
Les deux opérations que l’on doit pouvoir effectuer sur ces ensembles sont la comparaison — pour savoir si deux cellules appartiennent au même ensemble et sont donc connectées — et la mise en commun (union) de deux ensembles — lorsque l’on connecte deux cellules. (Voir plus loin les ensembles de Tarjan).
L’ouverture des murs dans le labyrinthe doit assurer qu’il existe un et un seul chemin reliant n’importe quelle cellule du labyrinthe à n’importe quelle autre.
Pour déterminer les murs à ouvrir, on s’intéresse à tous les murs à tour de rôle, dans un ordre aléatoire ; pour chaque mur, on regarde si les deux cellules qu’il sépare sont déjà connectées par un chemin, si ce n’est pas le cas, on l’ouvre.
En procédant de cette manière, on s’assure d’une part que toutes les cellules sont connectées entre elles — étant donné qu’on examine tous les murs à tour de rôle — et d’autre part que n’importe quelle cellule est reliée à n’importe quelle autre par au plus un chemin – étant donné qu’on n’ouvre un mur que lorsque les deux cellules qu’il sépare ne sont pas connectées.
L’idée de Robert Tarjan est de désigner pour chaque ensemble un élément qui représente tout l’ensemble. On appelle cet élément le représentant de l’ensemble.
Comparer deux ensembles revient alors à tester si leurs représentants sont identiques, tandis que mettre en commun deux ensembles revient à élire un nouveau représentant commun à ces deux ensembles.
A noter que cette technique fonctionne uniquement avec des ensembles disjoints deux à deux, c’est-à-dire ne possédant aucun élément en commun. Heureusement pour nous, les ensembles de cellules du labyrinthe satisfont cette propriété.
Pour mettre en œuvre les ensembles de Tarjan on considère également une structure ressemblant à un arbre : les éléments de l’ensemble sont représentés par un nœud qui contient une lien de type parent (qui contient l’adresse du nœud parent ou vide si le nœud est le représentant de son ensemble).
Pour rechercher le représentant d’un nœud, on consulte son champ parent. S’il est nul, alors le nœud est son propre représentant. Sinon, on répète l’opération en recherchant le représentant du nœud désigné par le champ parent. Etant donné que le nombre de nœuds est borné, il n’y a pas de cycles, on finira forcément par aboutir au représentant du nœud.
Les nœuds d’un même ensemble forment avec leur champ parent une sorte d’arbre dont la racine est le nœud qui représente l’ensemble. Plus un nœud est éloigné de la racine plus l’opération de recherche de son représentant est longue, car il faut parcourir un plus grand nombre de nœuds avant d’arriver à la racine.
Une optimisation très importante qui permet d’aplatir cet arbre, c’est-à-dire de réduire la distance entre les nœuds et leur représentant, est la suivante : après chaque opération de recherche du représentant d’un nœud, on parcourt une seconde fois les nœuds que l’on vient de parcourir lors de la recherche et on modifie leur champ parent pour qu’il contienne l’adresse de leur représentant. Ainsi, la prochaine fois que l’on recherchera le représentant de l’un de ces nœuds on l’obtiendra immédiatement sans devoir parcourir d’autre nœuds. Cette optimisation est représentée dans la figure ci-dessous :
Initialement, en (a), les quatre éléments appartiennent tous à des ensembles différents. Chaque élément est donc le représentant de son ensemble. En (b), les ensembles des éléments 1 et 2 sont mis en commun, et l’élément 2 est choisi comme nouveau représentant. En (c), ce sont cette fois les ensembles des éléments 3 et 4 qui sont mis en commun, et 3 est choisi comme nouveau représentant. En (d), les deux ensembles sont mis en commun, et 3 est à nouveau choisi comme représentant. Le contenu des ensembles reste le même en (e), par contre une optimisation d’aplatissement est appliquée afin que l’élément 1 ait le représentant de son ensemble, à savoir 3, comme parent direct. Cela élimine une indirection lors des recherches subséquentes du représentant de l’élément 1.
La solution actuellement proposée est donnée par les fichiers MatLab : labyrinthe.m.