Résumé : peut-on ou doit-on utiliser une calculette en classe ? Pour alimenter ce débat, Alex Bogolmony suggère de donner aux élèves une calculette endommagée et d’observer leur comportement : font-ils alors appel à leurs connaissances pour se débrouiller ? Ne doit-on pas inventer le mot innuméralisme pour qualifier l’impossibilité qu’ont certaines personnes à se débrouiller sans leur calculette ?
Mots-clés : calculette, innuméralisme.
L’exercice s’inspire du site Internet www.cut-the-knot.com de Alex Bogomolny.
Alex Bogomolny débute sa réflexion en prenant comme modèle Janus. Janus est un dieu italique et romain représenté avec deux visages opposés. Ses légendes sont uniquement romaines. Il aurait abordé en Italie où il aurait fondé une ville sur la colline qui prit de lui le nom de Janicule. Il aurait accueilli Saturne chassé de Grèce par Jupiter et civilisé les premiers habitants du Latium. A Rome, il est gardien des "portes". Son temple possède deux entrées fermées en temps de paix ; elles restent ouvertes en temps de guerre pour que le dieu puisse se porter au secours des Romains. Il ouvre et ferme l’année : le mois de janvier, Januarius lui est consacré.
Alex Bogomolny compare l’innovation technologique aux deux visages de Janus. Il prend comme exemple, le nucléaire qui offre à l’humanité une source abondante et bon marché d’énergie mais également, des moyens de destruction totale inimaginables.
Cette comparaison lui sert d’introduction à la réflexion sur la question controversée de l’usage de la calculette en classe. Certains estiment qu’elle est à l’origine de l’innuméralisme, néologisme construit sur le modèle de l’illettrisme mais pour les mathématiques. D’autres estiment qu’elle est nécessaire et utile.
Alex Bogolmony a alors une idée originale : fournir aux élèves une calculette endommagée. Il espère ainsi forcer les élèves à comprendre la nécessité des tables de multiplication et du calcul élémentaire.
Il imagine donc une calculette dont seules certaines touches sont utilisables. Evidemment, cette calculette ne peut pas servir de façon générale à tous les calculs traditionnels. En revanche, il est certainement possible d’obtenir tous les nombres de un à quinze avec les limitations induites par les défectuosités de la calculette.
Pour résoudre ce problème élémentaire, l’élève devra faire appel à un peu d’arithmétique.
Le but de cet exercice est de programmer — c’est plus économique que de casser des calculettes — une calculette endommagée : seules quelques touches sont fonctionnelles. On prendra, par exemple, une calculette qui n’affiche que le zéro, la touche pour obtenir le résultat, une touche d’effacement, quatre touches avec des chiffres de un à neuf, deux touches pour les opérations, une touche de changement de signe, une touche pour l’écriture décimale (la virgule).
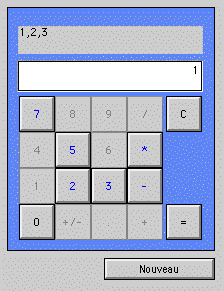
Sur le modèle des lancers de dés, il faut trouver un moyen de produire des nombres aléatoires. On choisit ensuite aléatoirement quatre chiffres entre un et neuf. On fait de même pour les opérations (on se contente de deux opérations) et pour les touches de changement de signe ou pour l’écriture décimale (la virgule).
Lorsque l’on enfonce les touches autorisées, un nombre est affiché sur l’écran de la calculette. Lorsque l’on choisit une opération, on l’enregistre et on passe à l’affichage du deuxième nombre. La touche d’obtention du résultat exécute l’opération enregistrée en prenant les deux nombres comme paramètres.
La solution actuellement proposée est donnée par les fichiers MatLab : calculette.m. La solution donnée par Alex Bogolmony est écrite en Java et se trouve sur son site.