Résumé : Clifford A. Pickover a imaginé une façon originale de mélanger fractals, chaos, graphisme sur ordinateur et science fiction. Suivant les paramètres, une infinité de représentations graphiques originales s’offrent à nous.
Mots-clés : fractals, chaos, attracteur.
L’exercice s’inspire du livre Chaos in Wonderland de Clifford A. Pickover, St. Martin’s Griffin, New York, 1994.
Pour les anciens, Chaos représentait l’inconnu, le monde spirituel menaçant, des visions de cauchemar qui reflétaient les peurs de l’homme devant l’irrationnel.
Aujourd’hui le chaos comprend l’étude de nombreux phénomènes sensibles aux conditions initiales. Cela signifie que si l’on modifie légèrement un paramètre d’une équation ou d’un système, un comportement différent peut se produire. On trouve des exemples de comportements chaotiques dans la fumée de cigarette, la météorologie, les activités cardiaques, etc.
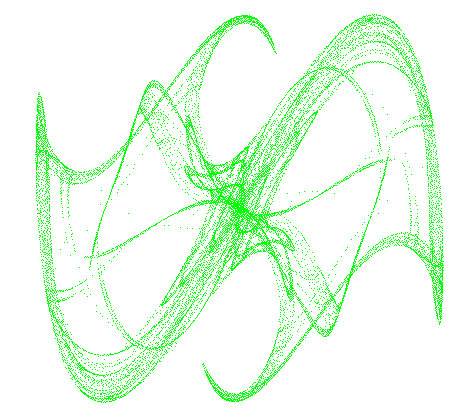
Un attracteur représente le comportement vers lequel un système est attiré. Une masse suspendue à une ficelle est attracteur sous forme de point fixe. Un attracteur étrange a un comportement irrégulier et imprévisible. Son comportement peut être représenté mais le graphique est beaucoup plus compliqué.
Un ordinateur est capable de simuler aisément le comportement des attracteurs étranges. Depuis on voit apparaître de nombreuses représentations originales dont, celles produite par Clifford A. Pickover.

Mathématiquement, la formule pour produire ces attracteurs est :
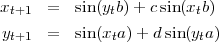
Dans l’exemple du Rêve du roi, les paramètres suivants ont été pris : a = -0.966918, b = 2.879879, c = 0.765145 et d = 0.744728.
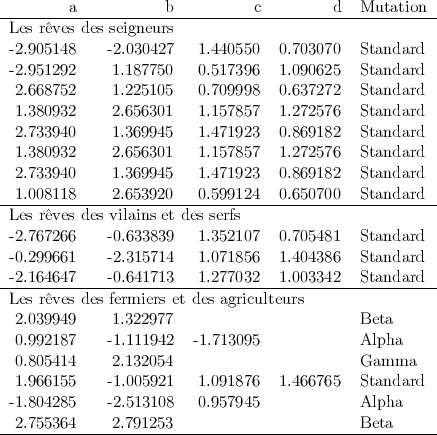
Ces équations peuvent être légèrement modifiées ; Clifford A. Pickover introduit alors la notion de mutation. La variation α est décrite par les équations suivantes :
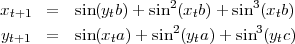
La mutation β est donnée par :
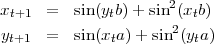

Et la mutation Γ par :
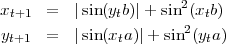
Clifford A. Pickover donne quelques valeurs utiles :
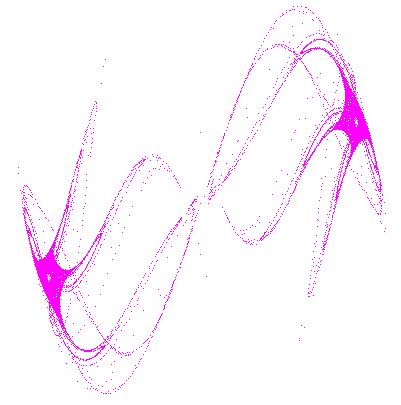
La solution actuellement proposée est donnée par les fichiers MatLab : pickover.m et demopickover.m.