Résumé : les planches à clous sont utilisées par les fakirs et par les statisticiens. Sir Francis Galton a imaginé une planche couverte de clous disposés sous forme triangulaire. En laissant tomber une bille sur le clou isolé au sommet du triangle, on observe un chemin aléatoire formé par les chocs successifs de la bille sur les clous restants. Combien de billes vont se retrouver aux extrêmités, au centre et ailleurs ? Le résultat obtenu ne surprendra pas les statisticiens qui reconnaîtront facilement la forme de la courbe résultante.
Mots-clés : aléatoire, statistique, courbe normale.
L’exercice s’inspire du livre Récréations informatiques, Pour la science, Belin, 1984 et du concours informatique organisé par l’olympiade suisse d’informatique en 2000.
Les nombres aléatoires jouent un rôle remarquable dans la simulation de processus. D’un point de vue philosophique, il est paradoxal que les nombres aléatoires, la plus pure expression de notre ignorance, nous aident à comprendre les systèmes complexes.
La simulation décrite ici s’inspire de la planche de Galton, baptisée d’après Sir Francis Galton, l’un des pionniers de la statistique, qui vécut à l’époque victorienne. Francis Galton est né le 16 février 1822 à Sparkbrook (près de Birmingham) en Angleterre ; il est mort le 17 janvier 1911 à Grayshott House, Haslemere dans le Surrey. Explorateur et anthropologue, Francis Galton est connu pour ses études pionnières sur l’intelligence humaine. Il consacra la dernière partie de sa vie à l’eugénisme (Définition du Larousse : l’ensemble des méthodes qui visent à améliorer le patrimoine génétique de groupes humains en limitant la reproduction des individus porteurs de caractères jugés défavorables ou en promouvant celle des individus porteurs de caractères jugés favorables. Outre le fait qu’il implique un jugement de valeur forcément discutable sur le patrimoine génétique des individus, l’eugénisme se heurte à la complexité du déterminisme génétique et de la transmission héréditaire des caractères physiques et mentaux, qui rend contestables ses fondements scientifiques et l’efficacité potentielle de telles méthodes. Historiquement, il a inspiré les pires formes de répressions et de discrimination, particulièrement dans l’Allemagne nazie).
Les idées de Galton influencèrent le développement des statistiques, particulièrement sa preuve qu’une association de distributions normales reste normale. Il apporta également d’importantes contributions à la météorologie et à l’anthropologie. Cousin de Charles Darwin, il était convaincu que la prééminence de différents domaines était dûe uniquement à des facteurs héréditaires.
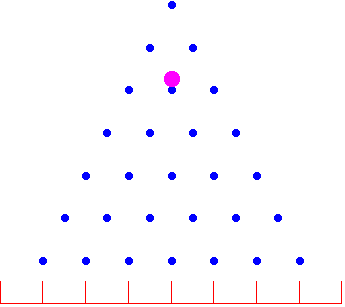
La planche de Galton est une planche inclinée comportant un réseau triangulaire de clous. On lâche successivement des billes à partir d’un point situé au-dessus du clou le plus élevé : elles se frayent un chemin entre les obstacles et on les récolte dans des cases disposées au bas de la pente. Lorsque la dernière bille arrive en bas, l’empilement des billes dans ces réceptacles dessine un profil caractéristique, qui ressemble à une courbe bien connue des statisticiens.
Tous les clous sont placés dans des lignes avec une distance constante entre eux. La première ligne contient un seul clou, chaque ligne consécutive contient un clou de plus. Les réceptacles ou paniers sont placés entre les clous de la dernière ligne. Un panier est rajouté à droite.
On peut organiser des paris : en lançant une bille sur le clou du haut et en n’intervenant d’aucune façon, la bille zigzague entre les clous ; à chaque lancement, les joueurs placent leurs paris dans un panier. Pour corser le tout, le responsable de la planche peut ôter certains clous (sauf sur la dernière ligne, celle du bas) ; les joueurs peuvent parier sur plusieurs paniers. Le but du jeu est alors de conseiller les joueurs sur les paniers pour maximiser leurs chances.
Le trajet de chaque bille est simulé, à l’intérieur d’une boucle, par une suite de nombres aléatoires (compris entre 0 et 1). Chacun de ces nombres correspond à un clou et permet de décider si la bille passe à droite ou à gauche de ce clou. Lorsque le nombre aléatoire est inférieur à 0.5, la bille passe à gauche et, dans le cas contraire, elle passe à droite. De quel clou s’agit-il ? Aucune importance ; il suffit d’augmenter d’une unité la valeur d’un compteur chaque fois que la bille passe à droite d’un clou.
Vous pouvez vérifier que le numéro de la case d’arrivée d’une bille ne dépend que du nombre de passages à droite des obstacles placés sur sa route. Il est donc inutile de faire figurer dans le programme un tableau qui représente individuellement chaque clou. La morale de cette observation est la suivante : un peu de réflexion économise de la mémoire (en tous cas, celle de l’ordinateur).
Une boucle plus générale simule la descente de plusieurs billes. On utilise cette fois un tableau : chaque fois qu’une bille est arrivée au fond, on augmente l’élément du tableau correspondant d’une unité. A la fin on représente le tableau sous la forme d’un histogramme.
Pour la deuxième version, il faut ajouter la gestion des paris.
Les solutions sont en cours de développement... Toute solution est la bienvenue.