Résumé : est-il possible de forer des trous de forme carrée ? Franz Reuleaux a donné une solution permettant d’effectuer des forages presque carrés. La figure qu’il a imaginée s’intitule triangles de Reuleaux ; elle comporte également d’autres propriétés intéressantes qui permettraient aux fabricants de boutons d’économiser de l’argent.
Mots-clés : triangle, largeur constante, barycentre, Reuleaux.
L’exercice s’inspire de l’émission Archimède Les triangles de Reuleaux du 3 novembre 1998, Arte.
Les sites Internet suivants traitent également du sujet :
Quelle doit-être la forme des boutons ? C’est par cette question que débute l’émission d’Arte consacrée aux triangles de Reuleaux. Un bouton doit pouvoir être enfilé dans une boutonnière quelle que soit sont orientation.
« C’est une erreur de croire que pour remplir cette tâche les boutons doivent obligatoirement être des disques », remarque le mathématicien allemand Reuleaux (1829-1905).
Franz Reuleaux suggère la construction d’un triangle équilatéral et de trois arcs de cercles centrés sur les sommets du triangle de rayon égal à un des côtés du triangle.
On peut mesurer la taille de cette figure à l’aide d’un pied à coulisse. Pour n’importe quelle position du triangle, on obtient toujours la même valeur, que l’on appelle le diamètre.
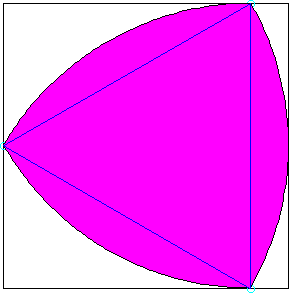
« Vous voyez, ajoute Reuleaux, qu’une courbe qui n’est pas un cercle peut avoir un diamètre constant ». Les boutonniers seraient bien inspirés de s’intéresser à de telles courbes : un bouton en forme de triangle de Reuleaux a une superficie plus petite que celle du bouton circulaire. Quel économie pour une efficacité identique.
Arte ajoute que les Britanniques ont utilisé cette propriété pour confectionner des pièces de monnaie (50 pences) dont les sept côtés du pourtour sont des arcs de cercle. Ces pièces peuvent être introduites sans difficulté dans les fentes des appareils à sous quelle que soit leur orientation.
Franz Reuleaux mettait en garde ses étudiants en mécanique de l’Institut royale de Berlin : « Faites très attention, si vous mesurez un cylindre avec un pied à coulisse et que vous obtenez toujours la même valeur, ce n’est pas pour cela que votre cylindre est circulaire. »
L’ingénieur britannique Harry Watts a inventé dans les années 1930, une fraise en forme de triangle de Reuleaux. Il disait dans ses dépliants publicitaires : « Qui croira que j’ai un outil qui peut percer des trous carrés ? »
Le but du problème est de représenter les triangles de Reuleaux et de démontrer ses intéressantes propriétés, notamment en les faisant tourner à l’intérieur d’un carré. La trace laissée par les sommets du triangle indiquera la forme du trou obtenu.
Une des propriétés du triangle de Reuleaux indique que la figure a une largueur constante. Cela signifie que la figure peut être tournée entre deux droites parallèles séparées par la dimension du côté. Puisque que le triangle de Reuleaux tient exactement dans un carré, que se passe-t-il lorsqu’on le tourne ?
Pour s’en convaincre, il peut être utile de découper dans du carton un triangle de Reuleaux, de percer un trou au centre de la figure et d’y glisser un crayon. En faisant tourner délicatement le triangle de Reuleaux on pourra observer la trace laissée par le centre lors de la rotation. La première réaction consiste à dire qu’il s’agit d’un cercle. Un peu de géométrie nous fera remarquer que la courbe est en réalité constituée de quatre morceaux d’ellipse.
Le triangle est équilatéral. La dimension du côté est donnée par s. On sait
alors que le point P qui est au centre du triangle a pour coordonnées x = s∕2 et
y =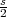 
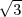. On déduit également AP =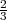 
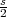
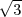et PB = s -
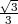s.
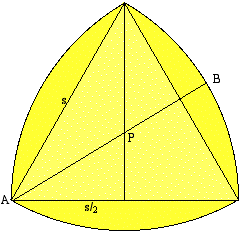
Comment trouver le chemin du barycentre du triangle de Reuleaux lorsqu’il
tourne dans le carré ? On suppose que le carré et le triangle ont des côtés
de dimension 1. On centre le carré à l’origine et on place le triangle de
Reuleaux de sorte que le sommet A est placé à (-1∕2;0). En utilisant la
formule donnée plus haut, on sait que le barycentre P a pour coordonnée
(-1∕2 +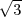 
;0).
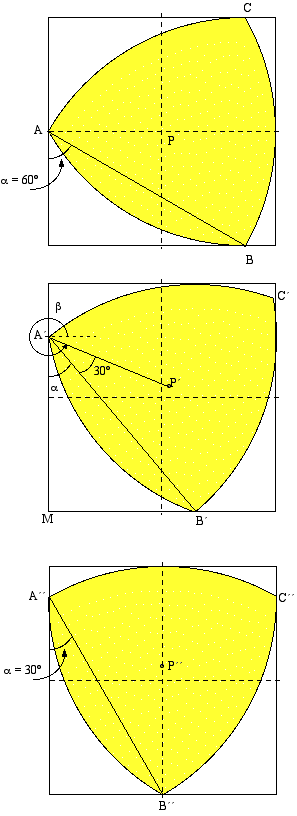
On imagine maintenant que le triangle tourne dans le sens des aiguilles d’une
montre ; on trouve le triangle A′B′C′ puis le triangle A′′B′′C′′. Le chemin de P à
P′′ est dans le premier quadrant. Soit α l’angle MA′B′, β l’angle formé par
A′P′ et une droite horizontale par A′, c la coordonnée y du point A′. On
recherche les coordonnées du point P′. On sait que cos(a) = 1∕2 + c et que
β = 3π∕2 + a + π∕6. On observe également que durant la rotation, a va de π∕3 à
π∕6. Comme A′P′ =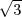 
∕3, les coordonnées x et y de P peuvent être
trouvées :
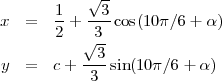
En simplifiant, on a :
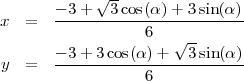
lorsque α passe de π∕3 à π∕6.
En recherchant le chemin du barycentre du triangle dans les trois autres quadrants, on trouve :
Pour le deuxième quadrant :
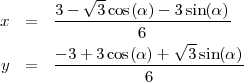
Pour le troisième quadrant :
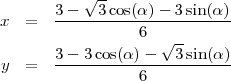
Et pour le quatrième :
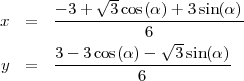
On remarque que ces équations ne décrivent pas un cercle !
On constate également que le trou est formé de coins arrondis. Quelle est alors la forme des coins ? Les équations sont les suivantes :
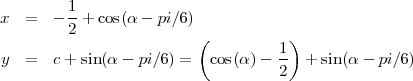
En simplifiant :
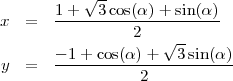
Ces coins sont en réalité des portions d’ellipse.
La solution actuellement proposée est donnée par les fichiers MatLab : reuleaux.m.