Résumé : Escher a effectué des recherches sur la répétition de motifs pour réaliser une de ses œuvres. L’ordinateur peut reprendre ces réflexions pour les reproduire.
Mots-clés : pavage, motif, rotation, translation, symétrie.
L’exercice s’inspire du livre Mathematica in Action de Stan Wagon, Springer Verlag, New York, 1999.
Un motif est un canevas remplissant un carré unitaire comme celui ci-dessous.
Escher eut l’idée de construire un pavé de dimension 2 × 2 en prenant quatre copies du motif et en tournant chacun d’un angle multiple de 90˚ . Ensuite, le pavé obtenu est utilisé pour paver ou remplir une surface plus grande.
Suivant la notation utilisée par Escher, les entiers 1, 2, 3 et 4 indiquent une
rotation (dans le sens des aiguilles d’une montre) de 0˚ , 90˚ , 180˚et 270˚ . Ainsi la
signature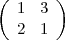 
donne le pavé ci-dessous.
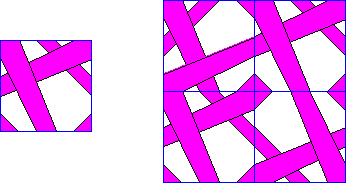
Escher utilisa le motif ci-après qui est basé sur un découpage 5 × 5 du carré
unité. La caractéristique principale du motif est qu’il couvre les quatre sommets
et les quatre points milieu des côtés. Il est relativement difficile d’imaginer ce que
la signature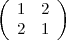 
pourrait donner.
Escher généralisa les signatures en introduisant la notation -n qui indique une rotation (comme n) suivie d’une réflexion par rapport à l’axe horizontal.
Il est évident que le nombre de signatures est de 44 = 256. Comme on peut
tourner le pavé final, chaque signature est équivalente à celle qui contient un 1 en
haut à gauche. Il reste donc au maximum 64 pavages différents. Mais de
nombreuses signatures conduisent à des pavages identiques. Par exemple, la
signature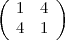 
est équivalente à 
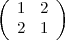via une rotation de 90˚ . Il y a
exactement 23 signatures différentes. Escher les connaissait. En incluant les
effets miroir par rapport à l’axe horizontal, on obtient 154 signatures
différentes.
En examinant le résultat d’une signature, on constate que l’effet de continuité
peut être modifié en changeant l’ordre d’apparition des couches. Escher
introduisit donc plus de variété en renversant simplement l’ordre d’apparition des
couches. Il plaça la lettre a devant le nombre dans les signatures pour indiquer le
renversement des couches. Ainsi, la signature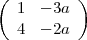 
représente
un pavé formé du motif initial, du motif tourné de 180˚ , réfléchi par
rapport à l’axe horizontal et avec renversement de l’ordre d’apparition des
polygones, du motif tourné de 270˚et du motif tourné de 90˚ , réfléchi par
rapport à l’axe horizontal et avec renversement de l’ordre d’apparition des
polygones.
Pour rendre le résultat plus spectaculaire, il serait également intéressant d’utiliser plusieurs couleurs. C’est la difficulté principale de ce problème étant donné que les transformations nécessaires pour interpréter les signatures d’Escher ne font appel qu’aux rotations, translations et symétries. Stan Wagon suggère l’utilisation d’équations pour résoudre le problème. Il faut alors nommer toutes les arêtes puis définir toutes les équations du pavage.
Pour colorier les pavages d’Escher, Stan Wagon suggère l’utilisation d’un tableau de dimension 2 × 2. Par exemple, le tableau
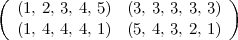
indique que le motif du coin en haut à gauche du pavé 2 × 2 utilise les cinq couleurs dans l’ordre ; la troisième couleur est utilisée par tous les cinq polygones dans le coin supérieur droit ; le coin inférieur gauche est colorié avec deux couleurs et le coin inférieur droit utilise les cinq couleurs dans l’ordre inverse.
Etant donné une signature, on place les différentes versions dans un pavé. On colorie chaque polygone différemment pour l’instant. Il faut fixer des couleurs identiques pour les polygones adjacents. Si l’on nomme toutes les variables on se trouve face au schéma suivant :
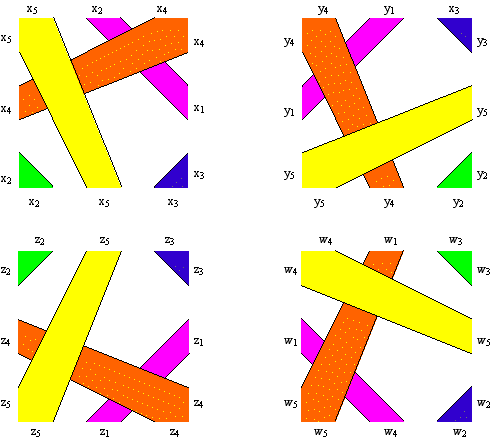
Les équations sont alors données par :
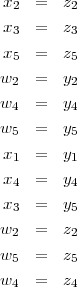
Il faut généraliser ces équations pour colorier correctement des pavages plus grands.
La solution actuellement proposée est donnée par les fichiers MatLab : defMotif.m et EscherPattern.m.