Résumé : Pendant onze années, la tsarine Maria reçut des œufs fabriqués par Fabergé. Les motifs qu’il utilisait étaient symétriques et répétitifs. Aujourd’hui, un informaticien amateur peut réaliser des motifs originaux ressemblant, modestement, aux décors des œufs de Fabergé.
Mots-clés : modulo, sinusoïde, ellipsoïde.
L’exercice s’inspire du livre Wonders of Numbers de Clifford A. Pickover, Oxford University Press, 2001.
Les œuvres d’art anciennes se caractérisent souvent par l’utilisation de motifs répétitifs et symétriques : les tapis persans, les vêtements, le carrelage, etc. Les œufs de Fabergé étaient fabriqués en or, argent, émail, pierres précieuses et peintures miniatures. Les plus connus furent commandés par le tsar. L’histoire débute en 1884 alors que Pierre Charles Fabergé fabriqua un œuf de Pâques commandé par le tsar Alexandre III pour son épouse, la tsarine Maria Feodorovna. Cet œuf devint légendaire et le tsar nomma Fabergé fournisseur impérial. Pour honorer sa charge, il devait créer un nouvel œuf chaque année. Pendant onze ans, la tsarine reçut un œuf, symbole de vie et de résurrection.
A la mort d’Alexandre, son fils Nicolas II poursuivit la tradition en commandant chaque année deux œufs à l’entreprise Fabergé. A Pâques, Fabergé en personne devait présenter un œuf à la douairière Maria Feodorovna pendant que son assistant devait présenter le deuxième à Alexandra Feodorvna, la femme de Nicolas. En tout, cinquante six œufs furent produits entre 1885 et 1917.

Le but du problème est de tenter d’approcher les merveilles de Fabergé en faisant appel aux outils mathématiques et informatiques pour décorer des œufs virtuels de façon originale.
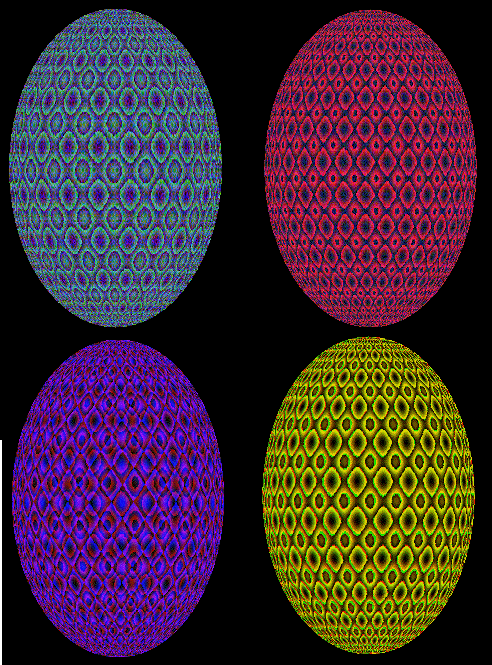
Les équations sinusoïdales fournissent un réservoir important pour les artistes en herbe. Les algorithmes décrits par Clifford A. Pickover permettent d’interagir avec les formes, les ombres et les couleurs pour produire des images classiques et futuristes.
Les motifs pour décorer les œufs peuvent être décrits de la façon suivante :
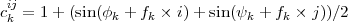
où les indices k ont les valeurs 1, 2 et 3, pour produire les intensités de rouge, vert et bleu avec, 1 ≤ i ≤ 400 et 1 ≤ j ≤ 400. Ceci permet de créer trois tableaux de dimension 400 × 400 avec des valeurs c contrôlées par les phases φ,(0 ≤ φ ≤ 1), ψ,(0 ≤ ψ ≤ 1), et les fréquences f,(0.15 ≤ f ≤ 0.8). Les valeurs des phases et des fréquences sont déterminées une fois pour chaque œuf.
Pour colorier les surfaces, les valeurs de ck sont multipliées par mk, tronquées et divisées par βk. Puis, on prend le reste de la division entière pour déterminer la couleur de la surface à la position i et j.
Il reste à représenter la surface de l’œuf et de la colorier suivant les motifs construits ci-dessus. On sait que la forme d’un œuf n’est pas définissable mathématiquement. On peut prendre une première approximation en construisant un ellipsoïde dont l’équation cartésienne est :
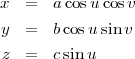
On peut également simuler l’éclairage par une source lumineuse en éclaircissant une partie du motif.
La solution actuellement proposée est donnée par les fichiers MatLab : demoFaberge.m..