Résumé : le puzzle est un jeu extrêmement répandu et connu. Mais, comment fabrique-t-on les pièces ? Les formes des pièces de puzzle sont en effet remarquables ; elles se ressemblent, tout en étant différentes ; lorsqu’elles s’emboîtent, elles ajoutent à la solidité de l’ensemble. Mathématiquement, il est possible de décrire la forme des pièces des puzzles. Avec un ordinateur, on peut même les représenter à volonté.
Mots-clés : spline, tangente, hasard.
L’exercice s’inspire de l’article Puzzling graphics in METAPOST de Hans Hagen, 1997.
Les origines des puzzles remontent aux années 1760 lorsque les fabricants de cartes de géographie sur bois eurent l’idée de les couper en pièces plus petites. Les cartes découpées sont encore utilisées dans l’éducation. Depuis cette époque, les adultes se sont intéressés aux puzzles : une véritable obsession est apparue aux alentours des années 1900. Des écrivains d’alors ont décrit la progression inexorable du fanatique de puzzle : du sceptique qui considère le puzzle comme idiot et enfantin, au joueur qui va jusqu’à renoncer aux repas pour placer juste une dernière pièce et enfin, au vainqueur qui place la dernière pièce aux petites heures de la nuit.
Les puzzles d’alors étaient un véritable défi. La plupart des pièces étaient découpées exactement sur les lignes colorées. Il n’y avait pas de pièce de transition avec deux couleurs témoin. Un éternuement ou un mouvement négligeant pouvait défaire des heures de travail parce que les morceaux n’étaient pas emboîtés. De plus, les puzzles ne comportaient pas d’image témoin sur l’emballage ; le titre pouvait être fallacieux et le sujet pouvait demeurer un mystère jusqu’à ce que les dernières pièces aient été placées.
Comme les puzzles étaient fabriqués en bois, ils devaient être découpés une pièce après l’autre. Ils étaient dès lors chers. Un puzzle de 500 pièces pouvait coûter près de 5 dollars, ce qui était bien au-dessus du salaire moyen mensuel d’un ouvrier en 1908.
Aujourd’hui la fabrication des puzzles a été automatisée. On peut observer que les pièces actuelles sont découpées de façon plus régulière ; elles s’emboîtent très bien ; elles se ressemblent beaucoup mais sont rarement interchangeables. Les courbes ne sont jamais brisées, etc. Ces propriétés sont le résultat d’un traitement mathématique des courbes. Le principe est simple : on prend des points fixes et quelques points de contrôle. On calcule ensuite une courbe qui passe par ces points en contrôlant étroitement la courbure (elle doit rester minimale afin d’éviter des cassures).
Le but du problème consiste à représenter les pièces d’un puzzle idéal avec des pièces toutes différentes mais similaires. Les programmeurs chevronnés pourront ajouter une image, la découper et permettre le placement des pièces de façon interactive.

Pour dessiner une pièce de puzzle, on peut considérer que les extrémités coïncident avec les points d’intersection d’une grille. Sur chaque côté d’un carré de la grille, on considère sept points de contrôle. Ceux-ci décident de la forme de la pièce. Il suffit d’introduire une composante aléatoire pour faire en sorte que les points soient placés différemment.
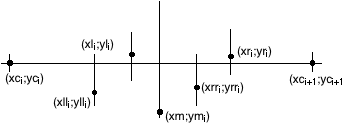
Les points (xci;yci) et (xci+1;yci+1) sont sur la grille. Le point (xmi;ymi) est le point milieu du segment. Les points (xli;yli) et (xri;yri) sont situés à 85% à gauche et 15% à droite du point central. Les points (xlli;ylli) et (xrri;yrri) se situent à 75% à gauche et 25% à droite du point central et au milieu de la hauteur entre xli et xlli. Il suffit d’ajouter ±10% aux coordonnées des points intermédiaires pour garantir des courbes différentes.
Il suffit ensuite de faire passer une courbe par tous ces points. L’interpolation qui permet de représenter au mieux une courbe lisse consiste à utiliser des splines. En quelques mots, un spline est une courbe qui passe par les points donnés et qui minimise la courbure. Il faut essentiellement faire attention à la façon dont les courbes se terminent. Pour garantir un comportement adéquat, les fonctions splines tiennent compte des tangentes : il suffit d’exiger que les tangentes soient nulles à gauche et à droite du spline.
Pour obtenir les courbes verticales, il suffit de faire une rotation de 90∘. Pour isoler des pièces il faut travailler par morceau.
La solution actuellement proposée est donnée par les fichiers MatLab : puzzle.m, puzzleDraw.m et demopuzzle.m.