Résumé : le maillage se dit Mesh en anglais. Il consiste à décomposer l’enveloppe d’un volume en polygones. De belles surfaces peuvent ainsi être représentées à l’aide d’un ordinateur.
Mots-clés : surface, grille, maillage, mesh, fonction implicite.
L’exercice s’inspire de sites internet dans lesquels des artistes non réfractaires aux mathématiques s’expriment en représentant des surfaces virtuelles originales : une banane, un coquillage, une fleur, un cœur, un instrument de musique nommé Kazoola, etc. (http://www.povray.org).
Un Kazoola est à la fois un jouet et un instrument de musique, trouvé dans une chambre d’enfant. Avant de le jeter définitivement, le père de l’enfant décide de le représenter à l’aide d’un logiciel de rendu 3D. Il s’aperçoit qu’en soufflant au travers d’un trou du jouet, il est capable de produire une réverbération d’au moins 120 décibels. Après d’autres recherches, il constate également que la surface peut être produite par un polynôme d’ordre six :
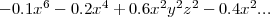
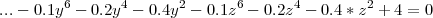

Pour représenter des objets réalistes, les principes sont les mêmes, on découvre des fonctions mathématiques qui définissent des surfaces. Souvent on les associe à leurs auteurs. On parle alors de surface de Dini, Enneper, Klein, Dupin, Boy, Kuen, Hunt, Kummer, Moebius, Cayley, Celbsch, Steiner, Costa, Barth, etc.
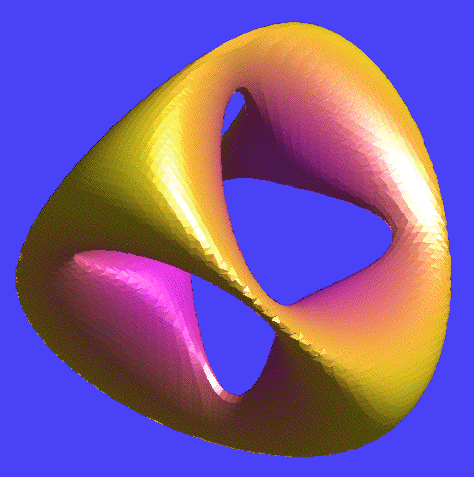




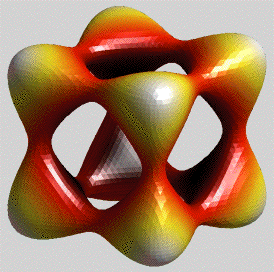
Le but de l’exercice est d’écrire un programme général permettant, quelle que soit la fonction mathématique donnée, de représenter une surface.
Pour représenter de telles surfaces, il faut disposer d’un logiciel capable d’afficher des portions de surfaces simples. Généralement, il s’agit de triangles ou de parallélogrammes.
La plupart des fonctions utilisées pour représenter les surfaces ci-dessus sont définies de façon implicite : on définit une fonction f pour chaque point de l’espace et l’on recherche les valeurs pour lesquelles la fonction est constante (p0).
Pour illustrer comment de telles surfaces sont obtenues, il est commode de considérer la même approche en 2D. On définit alors des courbes et non plus des surfaces. La fonction associe une valeur à chaque point (x;y) et peut être associée à une surface. L’intersection de cette surface avec un plan z = p0 est une courbe. C’est précisément ce que l’on recherche. La méthode proposée ci-dessous est celle de M. Beaudouin-Lafon, professeur d’informatique, dans un de ses devoirs d’informatique graphique.
Pour approximer cette courbe à 2D, on se donne une grille carrée et on calcule la valeur de la fonction en chaque point de la grille. Si la valeur de f est supérieure à p0, on marque le point de la grille en blanc, sinon en noir.
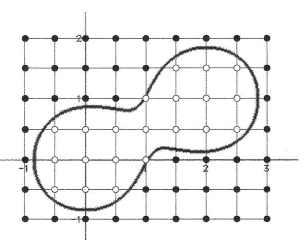
Pour chaque arête de la grille qui a des extrémités de couleur distincte, la courbe intersecte cette arête. Si l’on considère un carré de la grille, on a quatre cas possibles d’intersection (aux rotations et symétries près, y compris la symétrie qui échange points noirs et blancs). L’intersection de la courbe et du carré consiste en 0, 1 ou 2 segments.
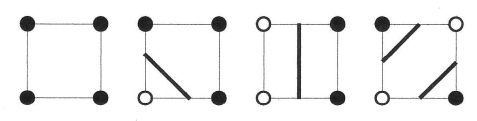
Il suffit alors d’assembler ces segments pour obtenir un contour polygonal, approximation de courbe cherchée.
En trois dimensions, l’algorithme procède de la même façon, mais avec une grille 3D : on découpe l’espace par une grille cubique et, on calcule l’intersection de la surface avec chaque cube de la grille. Chacune de ces intersections est approximée par une ou plusieurs facettes polygonales. Plus la grille cubique est fine, plus l’approximation de la surface est meilleure, mais plus le coût en calcul est élevé.
Pour calculer l’intersection de la surface avec un cube de la grille, on calcule la valeur de la fonction en chaque sommet du cube et on marque le sommet d’un blanc si la valeur dépasse p0 et d’un noir sinon.
Il existe 256 codes, correspondant à toutes les configurations possibles de l’intersection de la surface avec un cube. En éliminant celles qui sont identiques par rotation et/ou symétrie, on peut ramener ces configurations à 14 possibilités distinctes.
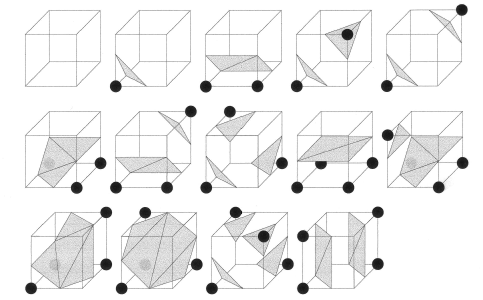
Pour chaque arête intersectée par la surface, on calcule la position du point d’intersection par interpolation linéaire.
Il suffit ensuite de représenter toutes les facettes obtenues.
Les expressions mathématiques permettant de représenter les figures données sont les suivantes :
La solution actuellement proposée est donnée par les fichiers MatLab : banane.m, barthsextic.m, dini.m, swisschease.m, chair.m, tangle.m, et surfcv.m Copyright (c) 1997 Ruslan L. Davidchack, University of Kansas, Lawrence, KS, davidchack@kuphsx.phsx.ukans.edu, http ://weizen.chem.ukans.edu/ruslan, created : Sep 29, 1997.