Résumé : les mécanismes horlogers sont constitués essentiellement d’engrenages. Ces derniers sont utilisés pour multiplier ou démultiplier une vitesse d’entrée pour obtenir une vitesse de sortie particulière. L’ordinateur peut aider à simuler le fonctionnement des engrenages.
Mots-clés : vitesse angulaire, engrenage, arbre, transmission.
L’exercice s’inspire de l’article Mathématiques des engrenages de Nicolas Terracol, Tangente Education no 82, septembre-octobre 2001.
Les engrenages ont de nombreuses applications : mécanisme horloger, boîte à vitesse, etc. Leur utilité réside essentiellement dans la fabrication de systèmes destinés à multiplier ou à démultiplier une vitesse d’entrée pour obtenir une vitesse de sortie particulière.
Le problème peut être posé comme suit : on dispose d’un arbre qui tourne à une vitesse angulaire donnée et plusieurs engrenages ; on désire obtenir en sortie une vitesse angulaire différente. Comment faut-il disposer les engrenages ?
Nicolas Terracol rappelle que les premières machines construites afin de modifier la vitesse angulaire étaient des roues de friction. Ces roues étaient lisses et construites dans une matière avec fort coefficient de frottement. Ce système ne permettait pas de contrôler correctement le rapport des vitesses car les frottements ne sont pas constants.
On a donc disposé des obstacles sous forme de dents autour des roues pour permettre une meilleure transmission entre elles.
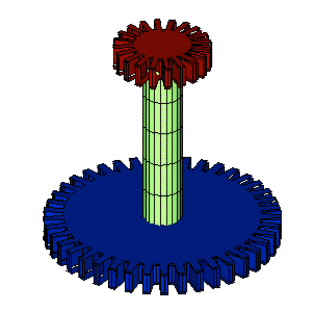
Un engrenage peut être défini par sa vitesse angulaire, son diamètre, son nombre de dents et par le pas de la denture. Il y a deux sortes d’engrenage : des roues simples et des roues simples réunies par un arbre.
Les mathématiques peuvent nous aider à résoudre le problème. On trouve alors rapidement la relation fondamentale qui existe entre deux, puis plusieurs engrenages. L’ordinateur permettra de visualiser ensuite un système formé de plusieurs roues et d’observer les vitesses obtenues.
Si l’on nomme, ω, la vitesse angulaire, d, le diamètre, n, le nombre de dents et p, le pas d’un engrenage, alors on a la relation suivante : pour engrener deux roues, les engrenages doivent avoir le même pas (on utilise une notation indicée pour différencier les caractéristiques de différents engrenages). On en déduit une relation entre la circonférence et le pas :
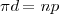
ou encore
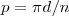
.
Comme les pas sont identiques, p1 = p2, alors
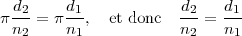
On en déduit qu’au point de contact de deux engrenages, les extrémités des dents ont la même vitesse linéaire mais, pas la même vitesse angulaire.
La vitesse linéaire se déduit de la vitesse angulaire et du rayon :
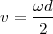
donc
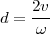
et ainsi,
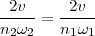
plus simplement,
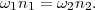
Le rapport d’un engrenage est défini par le quotient de la vitesse angulaire de sortie par la vitesse angulaire d’entrée. On obtient donc :
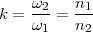
Plus simplement, on peut dire que le rapport des vitesses est le rapport inverse du nombre de dents.
On obtient alors la formule de base des engrenages :
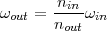
Lorsque l’on prend plusieurs couples d’engrenages, on s’aperçoit que les roues intermédiaires d’un engrenage n’ont aucune influence sur le rapport du montage. On n’aura donc qu’un nombre limité de rapports de réduction possibles.

Pour permettre d’autres rapports, on utilise des engrenages formés de deux roues couplées par un arbre. Les vitesses angulaires des deux roues couplées sont cette fois identiques. Dans un montage avec deux arbres, on constate que le rapport de réduction correspond au rapport des nombres de dents des roues qui se touchent (roues centrales).
On peut également démontrer par récurrence que le rapport total d’un montage est égal au produit des montages intermédiaires :
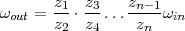
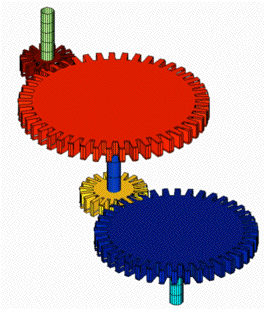
La solution actuellement proposée est donnée par les fichiers MatLab : engrenage.m, demoEngrenages.m et demoArbres.m.