Chapitre 99
Qu’importe le flocon

Résumé : qu’un Suédois s’intéresse aux flocons, cela n’a rien d’étonnant. Mais, il s’agit ici en réalité d’un mathématicien, Helge von Koch, qui fut le premier à exhiber une courbe fermée, continue, dérivable en aucun point, sans point double et de périmètre infini pour une aire inférieure finie. Cette courbe, appelée flocon de Koch ou flocon de neige, est une courbe fractale qu’un ordinateur peut facilement représenter.

Mots-clés : flocon, Koch, fractal, récursivité.

Enoncé

L’exercice s’inspire de nombreux sites Internet qui traitent du sujet, notamment :

• http://www.sciences-en-ligne.com/momo/chronomath/chrono/
  
• http://membres.lycos.fr/tpefractal/Flocon.htm?
  

De la carrière de Helge von Koch (1870-1924), on peut retenir qu’il a fait des études de mathématiques à l’Université de Stockholm auprès de Mittag-Leffler, qu’il fut enseignant au département de mathématiques de l’Institut royal de technologie de Stockholm puis à l’Université. Il fut le premier à exhiber (1904) une courbe fermée, continue, dérivable en aucun point, sans point double et de périmètre infini pour une aire intérieure finie.

Si l’on examine un flocon de neige naturel à différentes échelles, on observe une structure à peu près identique à celle du flocon de Koch.

On construit le flocon de Koch en reproduisant un triangle équilatéral à des échelles de plus en plus petites. En répétant ce processus une infinité de fois, la courbe obtenue possède alors un périmètre infini mais une aire limitée.

On démarre avec un triangle équilatéral et on découpe un tiers de chaque segment que l’on remplace par les deux côtés d’un triangle équilatéral dont le côté vaut le tiers du côté initial. En d’autres mots, on prend un côté AB, on le découpe en trois parties, on obtient les sommets C et D. L’arête CD permet de construire un nouveau triangle équilatéral avec un nouveau sommet E comme suit :

On constate rapidement que le diamètre devient infini mais que la courbe possède pourtant une aire intérieure finie.

Le but de l’exercice est donc de représenter et de calculer l’aire du flocon de Koch.

Indications

La récursivité est une méthode de programmation générale permettant à une fonction de s’appeler elle-même. Pour représenter le flocon de Koch, on peut procéder comme suit : la fonction dessine le segment AB, puis, calcule les points C, D et E comme indiqué ci-dessus ; la fonction s’appelle alors elle-même quatre fois de suite en prenant les segments AC, CE, ED et DB.

Cette récursivité peut s’exprimer ainsi : pour dessiner la courbe de niveau n, on découpe le segment selon le modèle ci-dessus, puis on dessine la courbe de niveau n - 1 pour chaque nouveau segment.

Un des principes de la récursivité consiste à indiquer évidemment la condition de fin (sinon les boucles sont également infinies). Ici il suffit de s’arrêter lorsque n vaut 0.

Pour calculer le périmètre et l’aire, on peut raisonner comme suit :

soit 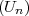le nombre de côtés, U_n = 3 × 4ⁿ,

soit 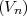la longueur d’un côté, V _n = ,

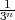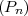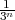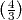soit le périmètre du flocon, P_n = U_n × V _n = 4 × 4ⁿ × = 3 ×ⁿ,

alors lim_n→∞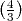ⁿ = +∞, car 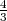> 1, donc lim_n→∞P_n = +∞.

L’aire d’un triangle équilatéral de base a est de a²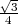, S₀ = 1² ×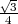

S₁ = S₀ + 3× aire d’un petit triangle avec aire = 1∕3.

En généralisant :

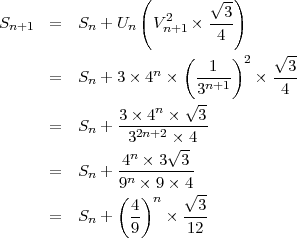
Par addition,

Donc,

Comme

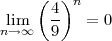
donc

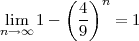
donc

donc

Solutions

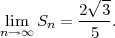
La solution actuellement proposée est donnée par les fichiers MatLab : demoKoch.m et koch.m. Elle est également donnée en Java : Koch.java, DrawJPanel.java, et DemoKoch.java. L’applet compilée peut être testée ci-dessous :