Résumé : Depuis que la ola mexicaine existe, on peut se demander comment la modéliser. Pourquoi part-elle souvent dans le même sens ? Comment la déclencher ? Comment la poursuivre ou non ? Le but de cet exercice est d’expliquer comment modéliser cette vague de spectateurs que l’on observe de plus en plus dans les stades sportifs.
L’exercice s’inspire de l’article Mexican waves in an excitable medium de I. Farkas, D. Helbing et T. Viscek, département de physique biologique, Eötvös, volume 419, 12 septembre 2002, Nature Publishing Group.
La vague mexicaine ou la ola, qui est devenue célèbre lors de la coupe du monde de football en 1986, surgit parmi les rangées de spectateurs dans un stade lorsque quelques spectateurs se mettent sur leurs pieds, lèvent leurs bras et ensuite s’asseyent à nouveau alors que les spectateurs voisins en font de même. Pour interpréter et quantifier ce comportement collectif, les auteurs de l’article ont développé plusieurs modèles en se basant, notamment, sur des enregistrements vidéo de vagues se déroulant dans des stades de football. Ils ont constaté que la vague se déplace généralement dans le sens des aiguilles d’une montre à une vitesse d’environ 12 mètres par seconde (ou 20 sièges) et a une largeur d’environ 6 à 12 mètres (une moyenne de 15 sièges). Elle est générée par moins d’une douzaine de spectateurs se levant simultanément et ensuite elle s’étend à l’ensemble de la foule lorsqu’elle acquiert une forme stable quasi linéaire.
La ola mexicaine peut être décomposée en deux phénomènes : la formation de la vague et sa propagation. La vague est formée habituellement par la levée simultanée d’un petit nombre de spectateurs. Des spectateurs se levant dans un groupe représentent une petite perturbation ou excitation, qui suivant leurs voisins, peut disparaître rapidement. Cette diffusion se produit seulement si le public se trouve dans l’humeur appropriée pour une vague : pas trop ennuyé ni trop excité non plus. En d’autres mots, le public devrait être assis mais, « excitable ». Si la perturbation est amplifiée alors, selon les observations faites en vidéo lors d’olas réelles, pendant un intervalle de temps très court (moins d’une seconde) la vague meurt sur un côté et survit sur l’autre. Les paramètres décrivant les réactions des spectateurs aux perturbations des voisins sautant sur leurs pieds sont expliqués plus loin.
La brisure spontanée de la symétrie observée durant la formation d’une vague est probablement due non seulement à la nature asymétrique de la perception chez l’homme mais également, aux attentes des spectateurs lors d’expériences précédentes à propos des olas mexicaines et autres comportements de foules. D’après les enregistrements vidéos, environ trois sur quatre vagues se déplacent dans le sens des aiguilles d’une montre alors que, une sur quatre se déplace dans le sens anti-horaire. Etant conscient de l’influence des phénomènes psychologiques et physiques lors de la brisure de la symétrie, les auteurs ont décidé d’utiliser le modèle le plus simple.
Le but du problème est de simuler une ola mexicaine. Pour obtenir des informations supplémentaires, il est conseillé de consulter le site Internet réalisé par les auteurs de l’article mentionné : http://angel.elte.hu/wave/.
Au temps t une personne i peut se trouver dans un des états suivants : inactif, actif ou réfractaire. Dans l’état inactif, une personne reste assise et peut être rendue active. Une personne active se lève et n’est pas influencée par d’autres. Dans l’état réfractaire, une personne s’assied ou reste assise en se remettant passivement de l’activité précédente. En résumé, les gens peuvent être influencés seulement depuis un stade d’inactivité et peuvent influencer d’autres seulement s’ils sont en activité.
Lors de la simulation, la mise à jour de la concentration pondérée des personnes actives à l’intérieur d’un rayon autour de chaque personne est comparée au seuil d’activation de chacun. Ensuite, si une personne est inactive, alors elle peut être activée selon le résultat de cette comparaison et selon les règles d’activation du modèle. Chaque personne dispose d’un temps de réaction τ pour mettre à jour la concentration pondérée des personnes actives autour d’elle.
Les poids sont proportionnels aux cosinus de l’angle de direction du vecteur partant de la personne inactive vers la personne active. Une personne immédiatement à la gauche d’une autre a une influence w0 fois (w0 < 1) aussi forte que celle immédiatement à droite. Les poids diminuent exponentiellement avec la distance : la longueur de l’amortissement est R et la fin est à 3R. La somme des poids est de un pour chaque personne.
Les auteurs utilisent une surface rectangulaire pour la simulation de 80 rangées de 800 colonnes de sièges. La simulation est visualisée en disposant les spectateurs de façon égale dans les tribunes.
Chaque personne regarde vers l’intérieur du stade. Le système de coordonnées est toujours local et est fixé sur la personne de sorte que le vecteur (1,0) pointe vers la gauche de la personne (parallèlement à la rangée dans le sens des aiguilles d’une montre, si on l’observe de dessus) et le vecteur (0,1) pointe à l’arrière de la personne (de façon radiale à l’extérieur du stat, si on l’observe de dessus).
L’angle formé par le vecteur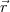 
ij, partant de la personne i vers la personne j
est φij. L’angle du vecteur (1,0) est φij = 0 et l’angle du vecteur (1,0) est
φij = π∕2. La longueur d’amortissement est R et l’amortissement cesse à 3R. Si
une personne jgauche se trouve à gauche d’une personne i et une personne jdroite
se trouve à sa droite alors, le rapport des forces d’influence entre jgauche et
jdroite est w0. Si l’on compare toutes les directions possibles, l’influence la plus
forte vient de la droite (la direction φij = π∕2) et l’influence la plus faible de la
gauche (la direction φij = 0) et entre deux l’influence varie avec le cosinus de
π - φij.
En résumé, le poids d’une personne j qui influence une personne i est :
![w = K -1exp(-|⃗rij|∕R)[1+ w + (1 - w )cos(π - φ )]
ij i 0 0 ij](am539x.png)
si 0 <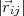 
< 3R et wij = 0 sinon.
La constante normalisée Ki est définie de telle sorte que la somme de tous les poids sur une personne valent 1 :
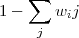
La concentration pondérée des personnes actives ressenties par la personne i est :
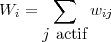
Dans tous les modèles, l’activation d’une personne i dépend de combien Wij dépasse le seuil d’activation pour cette personne ci. Le temps de réaction de la personne est τ ; c’est la différence de temps entre deux mises à jour de Wij.
La solution actuellement proposée est donnée en Java : Smilie.java, DessineDesSmilies.java, et DemoSmilie.java. L’applet compilée peut être testée ci-dessous :