Résumé : quel est le trajet parcouru par un cavalier qui part d’une case quelconque de l’échiquier, qui visite toutes les cases une et une seule fois et qui revient au point de départ ? C’est un problème ancien que l’on retrouve dans de vieux manuscrits consacrés aux échecs. Un peu de programmation permettra de s’apercevoir que la recherche de tous les coups possibles peut prendre énormément de temps ; il faut donc tenter de minimiser au maximum le nombre d’essais.
Mots-clés : circuit hamiltonien, Euler, graphe.
L’exercice s’inspire de plusieurs sites internet Récréomath, ChessBase et MATH.en.JEANS.
Le parcours du cavalier sur un échiquier est un problème ancien : il s’agit de déterminer un trajet parcouru par un cavalier qui part d’une case quelconque de l’échiquier et qui visite toutes les cases une et une seule fois. On exige parfois le retour sur la première case, on parle alors de parcours fermé (ou réentrant). Les questions qui sont apparues immédiatement étaient : est-ce que le cavalier peut effectuer un tel parcours et combien y a-t-il de solutions ?
Des réponses à la première question apparurent au neuvième siècle dans un manuscrit arabe par Abu Zakariya Yahya ben Ibrahim al-Hakim. L’auteur donne deux parcours, un par Ali C. Mani, un joueur d’échecs inconnu et l’autre par al-Adli ar-Rumi, qui connut ses heures de gloire aux alentours de l’an 840 et écrivit un livre sur le shatranj (une sorte de jeu d’échecs populaire à cette époque).
Pour retrouver un historique du jeu, il est recommandé de consulter l’excellent site internet : http ://homepages.stayfree.co.uk/gpj/ktn.htm.
La première analyse mathématique compréhensible du parcours du cavalier a été présentée au XVIIIe siècle par le mathématicien suisse Leonhard Euler (1707-1783) à l’Académie des sciences de Berlin en 1759. L’Académie avait proposé un prix de 4000 francs au meilleur mémoire sur le sujet mais, le prix n’a jamais été décerné, probablement parce que Leonhard Euler était à cette époque directeur du département de mathématiques de l’académie berlinoise. Il décrivait une méthode générale qui lui aurait été suggérée par Louis Bertrand (1731-1812), natif de Genève, mathématicien et géologue ; il était un disciple d’Euler avec qui il étudia plusieurs années à Berlin, il devint professeur de mathématiques à l’Académie de Genève, succédant à Jallabert et Tremblay.

Le nombre de parcours du cavalier possible sur un échiquier traditionnel est étonnamment grand. En 1995 Martin Löbbing et Ingo Wegener proclamaient que le nombre de parcours était de 33’439’123’484’294. Ce résultat a été obtenu en utilisant vingt stations de travail Sun pendant quatre mois.
En 1997 Brendan McKay utilisa une autre méthode pour obtenir le résultat : 13’267’364’410’532. Pour avoir une idée de ces nombres, un ordinateur cherchant des parcours à une vitesse d’un million par minute aurait besoin de plus de vingt-cinq ans pour les trouver tous.
Un parcours du cavalier magique est obtenu lorsqu’en numérotant chaque case, on trouve un carré magique. Des parcours magiques ne sont pas possibles sur des échiquiers n × n lorsque n est impair et, semble-t-il, également impossible sur un échiquier 8 × 8. On trouve des parcours semi-magiques (au nombre de 131) dans lesquels les sommes des diagonales ne sont pas vérifiées.
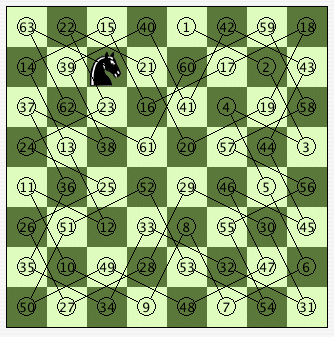
En février 2003 un enfant de neuf ans a fait sensation en Allemagne en participant à une émission télévisée : « Wetten dass.. ? » (Vous voulez parier ?). Le but de l’émission consiste à présenter devant les caméras des tours impossibles. L’enfant s’appelait Xaver Neuhäusler ; il venait de Bavière et présentait le pari de trouver un parcours du cavalier entièrement de tête en partant de n’importe quelle case de l’échiquier. Xaver avait les yeux bandés et une case de départ lui a été dictée. Sans aide, l’enfant dicta une suite de 64 cases formant un parcours du cavalier parfait. La réaction a été grande en Allemagne. Fallait-il donner des explications ou laisser croire à l’immense difficulté du problème ? En réalité, il suffit de mémoriser un parcours fermé et de l’expliciter en modifiant la case de départ.
Le but du problème consiste à représenter des parcours du cavalier et de trouver des solutions.
La première idée venue est de réaliser un programme qui parcourt un arbre de tous les chemins possibles. Comme on l’a vu plus haut, le nombre de solutions est beaucoup trop grand pour les trouver toutes. Pour chaque position du cavalier, on essaie les huit directions ; pour chaque direction possible on simule le saut, on sauvegarde la position dans un tableau et on effectue un appel récursif. Le problème de cette solution est qu’elle est extrêmement lente. On peut mettre en œuvre une solution plus efficace : on ne considère plus le parcours de l’échiquier comme un ensemble de cases à visiter mais comme un ensemble de liens ; ainsi, lorsque l’on arrive sur une case, on marque tous les liens qui y aboutissent ; il suffit alors d’éviter ces chemins. Le fait de couper à chaque mouvement les sauts possibles sur une case donnée diminue le nombre de possibilités (qui reste malgré tout très grand).
Il est intéressant de commencer par des échiquiers de taille réduite avant de tenter une généralisation. Dans un échiquier 2 × 2, il n’y a aucune solution, c’est évident. Dans le cas 3 × 3, le cavalier ne peut atteindre la case du milieu, c’est donc également impossible. Dans un échiquier 4 × 4, on peut indiquer dans chaque case le nombre de déplacements possibles :
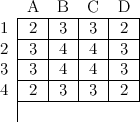
Le nombre dans chaque case donne la quantité de mouvements possibles. Exemple : de A2 on peut aller à C1, C3 et B4. On peut construire un graphe montrant toutes les relations entre ces mouvements. Avec ce modèle on peut imaginer les mouvements du cavalier dans le cas où on supprime les cases : sans les cases d’angle on supprime les cellules du centre du graphe (on continue à pouvoir faire le tour en périphérie et au centre) ; sans en plus, les cases du centre, on continue à pouvoir faire le tour (ou deux tours selon la position de départ). Avec ce genre de graphe, on peut montrer que le parcours du cavalier est impossible avec un échiquier 4 × 4. On peut aisément observer également qu’il n’y a aucun parcours passant par les quatre coins.
Pour un échiquier 5 × 5, c’est possible mais il est impossible de revenir au point de départ (aucun parcours fermé) :
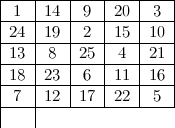
On peut également s’intéresser à des échiquiers rectangulaires. Dans un rectangle 3 × 4 (le plus petit possible), on a le parcours non fermé suivant :
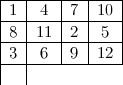
Au début du XIXe siècle, H. C. Warnsdorff présenta une méthode pour trouver rapidement un parcours du cavalier dans son ouvrage Des Rösselsprungs einfachste und allgemeinste Lösung, Schmalkalden, 1823. Le but est d’éviter les cases en cul-de-sac desquelles le cavalier ne peut s’échapper. Pour cette raison, les cases possibles pour le prochain déplacement sont examinées auparavant. On dénombre les possibilités d’accéder à chaque case et on se déplace alors vers la case possédant le plus petit nombre possible d’accès. Cette règle est heuristique. Théoriquement, on peut trouver des objections mais sur un échiquier standard, la règle de Warnsdorff fonctionne à merveille.
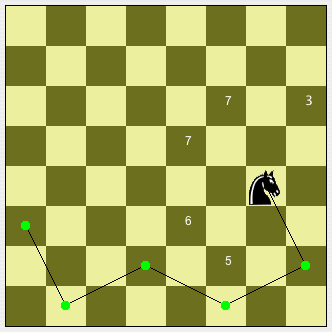
Si l’on considère une case dans un angle de l’échiquier alors, un cavalier ne dispose que de deux cases possibles pour se déplacer. Une case d’angle ne peut être atteinte que depuis deux cases de l’échiquier. Dans un parcours, lorsque le cavalier atteint une des deux cases mentionnées, il est obligé de visiter la case d’angle ; si le cavalier ne l’avait pas fait, il aurait utilisé une de deux entrées vers la case d’angle et ainsi l’aurait placé dans un cul-de-sac ; la case d’angle pourrait encore être atteinte mais le cavalier ne pourrait plus repartir.
Cette méthode nous donne des solutions mais, pas toutes les solutions. Le processus contient un peu d’arbitraire : il y a parfois un choix à faire entre plusieurs possibilités équivalentes. Elle n’est malheureusement pas généralisable à toutes les dimensions.
La solution actuellement proposée est donnée en java :
Echiquier.java, EchiquierP.java, et DemoEchiquier.java. L’applet compilée peut être testée ci-dessous :