Résumé : Comment placer trente-six officiers de six grades différents dans six régiments disposés en six lignes et six colonnes ? C’est la question que s’est posée Léonard Euler en 1782. Il constata rapidement qu’il n’y avait aucune solution. Il crut alors pouvoir généraliser son constat en conjecturant qu’il n’y avait pas de telles dispositions pour 4k + 2 avec k ≥ 1. Il donna également le nom de carré gréco-latin à ces tableaux. Cette conjecture a tenu jusqu’en 1959, où un carré gréco-latin d’ordre 10 a enfin été trouvé. Le but de l’exercice est d’utiliser l’ordinateur pour en trouver.
Mots-clés : carré gréco-latin, carré latin, carré magique.
Comment placer trente-six officiers de six grades différents dans six régiments disposés en six lignes et six colonnes ? C’est la question que s’est posée Léonard Euler en 1782. Il constata rapidement qu’il n’y avait aucune solution. Il crut alors pouvoir généraliser son constat en conjecturant qu’il n’y avait pas de telles dispositions pour 4k + 2 avec k ≥ 1.
Il donna également le nom de carré gréco-latin à ces tableaux. L’origine du nom vient du fait que les carrés trouvés par Euler étaient représentés sous forme de paires de lettres, l’une latine, l’autre grecque. Cette conjecture a tenu jusqu’en 1959, où un carré gréco-latin d’ordre dix a enfin été trouvé.

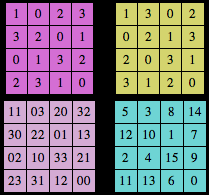
Un carré gréco-latin d’ordre n est un tableau de dimension n par n avec n couples de motifs répartis de manière qu’ils ne se trouvent qu’une seule fois dans chaque ligne et chaque colonne. Il y a donc n2 couples. Un carré latin d’ordre quatre est relativement bien connu : il s’agit de disposer seize cartes à jouer parmi les as, rois, reines et valets avec les couleurs, cœur, pique, trèfle et carreau. Dans l’exemple ci-dessous, on a deux carrés latins orthogonaux en haut, un carré gréco-latin en bas à gauche et un carré magique en bas à droite. Un carré latin est une grille carrée d’ordre n dans laquelle les cellules contiennent n lettres, nombres ou symboles, appelés éléments, qui sont disposés de telle manière qu’ils apparaissent une et une seule fois sur chaque ligne et dans chaque colonne. Un carré latin d’ordre n est orthogonal à un autre de même ordre si la superposition des éléments de cellules correspondantes conduit à un arrangement carré des n2 paires possibles. Les deux carrés latins du haut sont orthogonaux. Cet arrangement est appelé carré gréco-latin. Pour obtenir le carré magique, on convertit de base quatre à base dix les nombres apparaissant dans le carré gréco-latin (on passe de 11 à 1 × 4 + 1 = 5).
Contrairement à ce que pensait Euler, il existe des carrés gréco-latins d’ordre quelconque sauf pour deux et six. La non-existence de carrés gréco-latins d’ordre six a été définitivement confirmée en 1901 par la mathématicien français Gaston Tarry qui fit l’énumération exhaustive de tous les arrangements possibles de symboles. Cinquante-huit ans plus tard, en 1959, avec l’aide d’ordinateurs, deux mathématiciens américains, Bose et Shrikhande trouvèrent des contre-exemples à la conjecture d’Euler. La même année, Parker trouva un contre-exemple d’ordre dix. En 1960, Parker, Bose et Shrikhande démontrèrent que la conjecture d’Euler était fausse pour tous les n ≥ 10.

Les applications des carrés gréco-latins sont assez vastes : agriculture, économie, statistique, modélisation et même, littérature. Guy Chouraqui, lors du colloque de Cerisy, Mathématiques et psychanalyse, en septembre 1999 expliquait un utilisation originale faite par Georges Perec :
«En 1967, Perec, qui avait publié le roman Les choses, récompensé par le prix Renaudot, est coopté comme membre de l’Oulipo, cet Ouvroir de littérature Potentielle créé en 1960 par Raymond Queneau et François Le Lionnais, donc sous le double signe de la littérature et des mathématiques. Ce groupe s’assignait un double but : partir de textes existants pour en créer de neufs, ou bien partir de structures abstraites pour engendrer des textes ; dans une certaine mesure, La vie mode d’emploi s’inspire de ces deux principes. Dans le cadre de l’Oulipo, le mathématicien Claude Berge proposa en 1967 d’utiliser une structure combinatoire, le carré gréco-latin, que l’on désigne aussi par bi-carré latin, comme structure romanesque. Cette structure fournissait en effet, de manière appropriée, l’unité et la variété indispensables à l’œuvre littéraire.
«L’emploi de ce type de structure mathématique dans la création romanesque part du principe que l’art utilise nécessairement une combinaison d’éléments préexistants, formes, couleurs, lettres, mots – tout comme le monde naturel procède de l’agencement de briques élémentaires : particules, atomes, molécules... C’est ainsi que dans le Cahier des charges que Perec assigne au(x) roman(s) La vie mode d’emploi, existent 42 listes affectées à différentes catégories aussi diverses que la longueur des chapitres, le nombre et la position des personnages, le style des meubles, les citations littéraires ou les allusions picturales. Chaque liste comporte dix éléments, et les regroupements de ces éléments dans les chapitres du roman sont assurés de ne jamais se répéter par l’application de vingt-et-un carrés gréco-latins d’ordre dix réglant les couplages entre les vingt-et-une paires de listes. Parmi les listes figurent des règles paradoxales, Manque (qui annihile la contrainte associée) et Faux (qui remplace une contrainte par une autre). Et bien sûr, dans certains cas le Manque vient à manquer, et le Faux à être faussé, rétablissant ainsi l’intégrité de la contrainte qui leur est couplée, comme en application du principe de Pierre Dac selon lequel ”Une erreur peut être vraie ou fausse selon que celui qui l’a commise s’est trompé ou non en la faisant” !
«Cette complexité fascinante, et présentée par Perec de manière très visuelle, colorée et agrémentée de dessins, même s’il n’avait sans doute pas songé que ses outils de travail personnels pourraient être un jour intégralement publiés, se complète d’autres règles – et les connaît-on toutes ? Par exemple, le roman se déroule dans un immeuble comprenant 100 espaces (pièces, couloirs, escaliers, etc.) et Perec a voulu que chaque chapitre s’ouvre dans un de ces lieux, en respectant le parcours, capricieux mais parfaitement déterminé, d’un cavalier de jeu d’échecs visitant tour à tour toutes les cases d’un tableau de dix fois dix cases.
«Et afin que, en bonne règle gnostique, le macrocosme se conforme au microcosme, le livre se compose de quatre-vingt-dix-neuf chapitres seulement, car une petite fille entrevue au cours du roman a grignoté le coin d’un petit-beurre Lu... Il n’est bien sûr pas indifférent que ce gâteau, icône en abîme du roman lui-même, soit ”lu”. Mais cette dénomination est largement surdéterminée, comme l’a très finement démontré Claude Burgelin, parce que Lu est l’acronyme de Lefèvre-Utile, et que le psychanalyste de Perec, dans la période précédant immédiatement la composition de ”La vie mode d’emploi” était J.-B. Pontalis, à qui il convient de rendre son nom complet : Jean-Bertrand Lefèvre-Pontalis !
(...)
«Pourquoi tant de chapitres arborent fièrement dans le cahier des charges leur 42/42 de contraintes satisfaites, comme une note, comme un label de qualité ? Que représentaient au juste ces contraintes pour Perec ? Que dit-il, lui-même, du rôle de ces processus formels ? D’abord, l’esprit de jeu : ”les seuls énoncés me semblent avoir quelque chose d’alléchant : Polygraphie du cavalier (adaptée, qui plus est, à un échiquier de 10 x 10), pseudo-quenine d’ordre 10, bicarré latin orthogonal d’ordre 10”. D’autres fois, Perec invoque la catalyse de l’imagination, la mise à feu de la fusée de l’écriture, la ”pompe à imagination” : ”À partir de là, je faisais entrer dans le livre tout ce que je voulais raconter : des histoires vraies comme des histoires fausses, des passages d’érudition complètement inventés, d’autres qui sont scrupuleusement exacts. Le livre est devenu une véritable machine à raconter des histoires, aussi bien des histoires qui tiennent en trois lignes que d’autres qui s’étalent sur plusieurs chapitres.” (...) Mais peut-on le croire totalement, quand on a pris la mesure du rôle réel de la contrainte dans son roman ?»

On ne connaît pas de méthode simple pour fabriquer automatiquement des carrés gréco-latins d’ordre pair. C’est la raison pour laquelle il a fallu attendre longtemps avant de trouver un premier carré d’ordre dix. En revanche pour les carrés d’ordre impair on peut trouver une méthode très simple qui en fournit quelques exemplaires.
En coloriant des carrés où chaque lettre est remplacée par une couleur (la même pour α et a, pour β et b, etc.), on obtient de magnifiques représentations graphiques comme celle ci-dessus.
Certains carrés gréco-latins sont plus faciles à construire que d’autres. C’est le cas notamment des carrés d’ordre impair. Prenons l’exemple du carré d’ordre cinq. On commence en prenant pour première ligne ABCDE. La dernière lettre de la ligne, E, débute la deuxième ligne qui est complétée par les lettres dans l’ordre (EABCD). On permute ce motif pour la troisième ligne (DEABC) et ainsi de suite pour former un carré latin. La même procédure est appliquée avec des nombres dans l’ordre inverse. La première ligne est alors 54321 et la deuxième 43215. Les deux carrés latins formés de lettres et de nombres sont ensuite superposés pour former un carré gréco-latin.
En permutant deux colonnes ou deux lignes d’un carré gréco-latin, on obtient à nouveau un carré gréco-latin. Ce principe est utilisé pour afficher des carrés gréco-latins au hasard en permutant plusieurs fois deux colonnes et/ou deux lignes.
On peut ensuite afficher les carrés gréco-latins sous forme de lettres ou de façon plus spectaculaire en coloriant une grille formée de carrés emboîtés : le grand carré est rempli d’une couleur correspondant à une lettre et le petit carré est rempli d’une autre couleur correspondant à un chiffre. La couleur du 1 et du A est la même. Le résultat est affiché plus haut dans l’énoncé. Avec un peu d’animation, on peut faire défiler les carrés gréco-latins avec des coloriages aléatoires.
La solution actuellement proposée est donnée par les fichiers MatLab : grecolatin.m. Elle est également donnée en Java : GrecoLatinApplet.java, GrecoLatinPanel.java, et GrecoLatin.java. L’applet compilée peut être testée ci-dessous :