Résumé : tout a été dit sur ce jeu qui fait fureur. Pourtant la manipulation de ces grilles est un excellent exercice, notamment pour ceux qui désirent apprendre le fonctionnement des matrices.
Mots-clés : grille, matrice, arithmétique modulo, combinatoire.
L’exercice s’inspire de l’article Le tsunami du Sudoku de Jean-Paul Delahaye, Pour la science, N∘ 338 , décembre 2005 et de nombreux sites internet consacrés au jeu.
Le nom Sudoku utilisé en occident provient des mots japonais Su = nombre et Doku = seul. Or ce jeu est nommé le plus souvent Number place au Japon. Les règles en sont simples. Une grille carrée de 81 cases est divisée en 9 carrés plus petits de 9 cases chacun ; nous les nommons les sous-carrés. Dans certaines des 81 cases, des chiffres sont inscrits au début de la partie. Il faut remplir les cases vides, en utilisant les chiffres de 1 à 9, de façon qu’aucun chiffre n’apparaisse deux fois dans la même ligne, ou deux fois dans la même colonne, ou deux fois dans le même sous-carré. Selon les canons du Sudoku, la solution doit être unique.
Plus qu’un jeu de chiffres, c’est un jeu de combinaisons et pour réussir il ne faut qu’une logique implacable et obstinée.
L’histoire du Sudoku se raconte comme une fable. Celle d’un juge néo-zélandais, Wayne Gould, retiré en Asie, qui découvre le jeu au Japon en 1997 et qui passe six ans à imaginer un logiciel permettant de créer de nouvelles grilles. A l’automne 2004, il vend sa trouvaille au Times puis à une soixantaine d’autres journaux dans une vingtaine de pays. C’est donc l’informatique qui a permis le succès de l’été. Parce qu’il n’y a aucune opération à faire, le Sudoku s’apparente à la combinatoire, la science du dénombrement et de la classification des configurations. Le Sudoku est de la famille des carrés latins : disposer un certain nombre de chiffres (neuf par exemple) dans une grille 9 × 9 cases afin que les chiffres ne se répètent jamais sur une même ligne ou sur une même colonne. Le carré latin peut se compliquer. On parle de carré gréco-latin quand on superpose deux carrés latins pour former des couples de chiffres, qui, eux également, ne doivent se répéter qu’une seule fois dans la grille. Malgré leur nom, il est peu probable que les carrés latins ou gréco-latins aient été utilisés dans l’Antiquité.
L’un des précurseurs de la combinatoire est le Bâlois Leohnard Euler (1707-1783), un génie des maths, auteur d’une quantité considérable de travaux. « Sudokiste » avant l’heure, il posa notamment le problème des « trente-six officiers ». Le voici : prenez une assemblée de 36 officiers, de six différents grades et issus de six régiments différents. Comment peut-on les ranger dans un carré, de manière que les officiers de chaque ligne et de chaque colonne soient de grade et de régiment différents ?
Ce problème donne plus de fil à retordre que le Sudoku « diabolico » que livre en pâture le Corriere della sera chaque dimanche à ses lecteurs. En trois siècles, il n’a jamais été résolu. Car il ne peut pas l’être. Le problème doit passer par résolution d’un carré gréco-latin à six cases de chaque côté. Euler soupçonnait que son problème était une colle. Il a fallu attendre 1901 pour que le mathématicien français Gaston Tarry démontre que le carré gréco-latin d’ordre 6 n’avait pas de solution... Leonhard Euler s’est attaqué à une énigme sur laquelle avaient séché beaucoup de mathématiciens avant lui. Comment peut-on faire parcourir à un cavalier toutes les cases d’un échiquier, mais qu’une fois chacune en respectant son mouvement ? Le Bâlois a trouvé la solution et l’a publiée en 1759 dans les « Mémoires de l’Académie des Sciences de Berlin ». Pour les Anglais, notre Leonhard Euler est bien le précurseur du Sudoku.
Leonhard Euler devait être pasteur, comme son père. Il est devenu l’un des plus grands mathématiciens de l’histoire. Son apport a été considérable dans le domaine des mathématiques, mais aussi de l’astronomie, de la mécanique, de la physique, de l’optique et de l’acoustique notamment. Diplômé de la Faculté de philosophie à 18 ans, Euler déposa sa candidature à l’Université de Bâle pour une place de professeur de physique. Mais on la lui refusa. Leonhard Euler partit alors pour Saint-Pétersbourg, où deux acolytes, Nicolaus et Daniel Bernoulli avaient été invités par l’Académie des Sciences. C’est là qu’il publia la moitié de ses travaux, l’autre paraîtra à Berlin pendant les vingt-cinq ans qu’il passa à l’Académie des Sciences dès 1741. Mais Euler, profondément pieux et attaché aux valeurs de l’Eglise réformée, ne partageait pas les idées voltairiennes, soutenues par Frédéric II. En 1766, le savant bâlois retourna à Saint-Pétersbourg. Aveugle dès 1771, mais encore très actif, il est mort en 1783. Il y a quarante ans, son tombeau a été transporté au cimetière du monastère Alexandre-Nevski.
Discussion sur le problème de l’énumération de toutes les grilles de Sudoku. Le nombre de carrés latins possibles de 9 × 9 est :
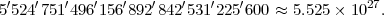
Ce nombre est énorme et il est évidemment impossible même avec un ordinateur d’obtenir une réponse dans un temps de calcul raisonnable. Bertrand Felgenhauer du département d’informatique de l’Université de Dresde a fait le calcul jusqu’au bout et il arrive à la conclusion qu’il y a :
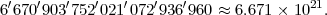
grilles valides de Sudoku. Quand on ne compte qu’une seule fois les grilles se déduisant les unes des autres par des opérations simples, le nombre de grilles complètes est légèrement inférieur au nombre d’humains sur la Terre (précisément : 5’472’730’538). Ce décompte devrait cependant rassurer les amateurs de Sudoku qui n’ont pas à craindre la pénurie de problèmes : même à raison d’une grille résolue par minute, une vie de cent ans n’en épuisera à peine qu’un pour cent.
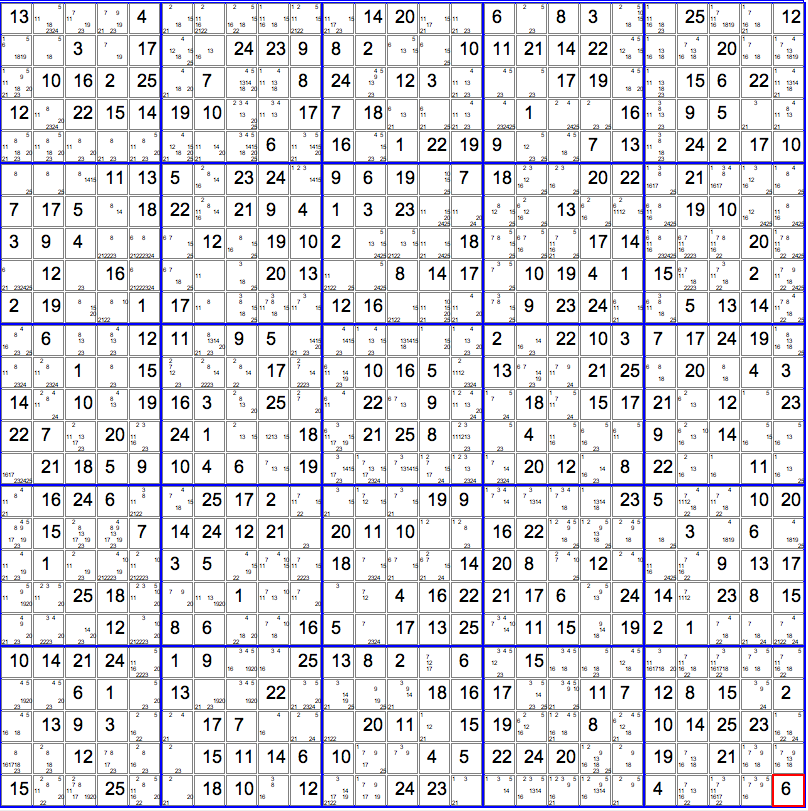
On peut considérer qu’une grille d’énoncé n’est intéressante que si elle ne peut être rendue plus petite, –c’est une grille minimale– c’est-à-dire que si elle possède la propriété suivante : dès qu’on enlève un chiffre de la grille d’énoncé, la solution n’est plus unique. Un autre problème de grille minimale est irrésolu aujourd’hui : quel est le plus petit nombre de chiffres à placer dans une grille pour que la solution soit unique. On connaît des grilles satisfaisantes avec 17 chiffres au départ ; on n’en connaît pas avec 16.

Il existe désormais de nombreuses variantes du Sudoku : grilles avec coloration des cases, grilles avec sous-carrés remplacés par d’autres formes, grilles de tailles différentes, grilles chevauchantes, etc.
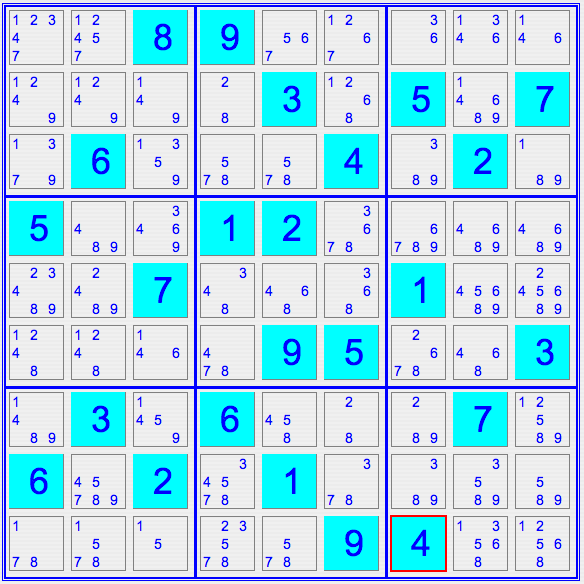
Le but du problème est de programmer une application permettant de contrôler le jeu. Pour ceux qui désirent connaître la solution du Sudoku, des méthodes de résolution peuvent également être mises en œuvre.
Il est relativement aisé d’écrire des programmes informatiques qui viennent à bout de toutes les grilles d’énoncés. Plusieurs méthodes sont envisageables, mais la plus courante est celle du « retour arrière systématique » (backtracking). L’idée est la suivante : le programme place le chiffre 1 dans la première case vide. Si ce choix est compatible avec les règles de base, il continue avec la seconde case vide où il place un 1, puis avec la troisième, etc. Lorsqu’il rencontre une incompatibilité (ce qui se produit rapidement), il augmente le dernier chiffre placé d’une unité et repart en avant.
Si, en voulant monter d’une unité le dernier chiffre placé, il découvre que c’est un 9, alors il revient en arrière et augmente d’une unité l’avant-dernier chiffre placé, puis repart en avant, etc. Bien programmée, cette méthode explore toutes les hypothèses possibles sans en oublier une seule, et donc, finit par trouver la solution lorsqu’elle existe.
Certains programmes ont aussi été écrits qui tentent de suivre de près les méthodes humaines : ils sont plus longs que les autres, mais aussi efficaces. Ces programmes, simulant le raisonnement humain, sont utiles pour mesurer la difficulté des grilles d’énoncés : selon les principes du raisonnement qu’il faut mettre en œuvre pour venir à bout d’une grille, elle est classée facile, moyenne, difficile ou diabolique.
Les grilles sont fabriquées actuellement presque toutes par des programmes qui fonctionnent sur l’idée suivante : on place les chiffres au hasard sur une grille et l’on applique un algorithme de résolution. Si la grille possède une solution unique, c’est terminé. Si la grille partielle aléatoire ne possède pas de solution, on lui enlève un chiffre et l’on recommence. Si elle en possède plusieurs, on en choisit une et l’on ajoute à la grille partielle autant de chiffres nouveaux nécessaires pour que la solution choisie devienne unique.
Parmi les méthodes de résolution classiques, on peut citer :
La solution actuellement proposée est donnée en Java : SudokuJApplet.java et SudokuJPanel.java. L’applet compilée peut être testée ci-dessous :