Résumé : comment construire une sphère ? Une solution réside dans la construction d’un polyèdre convexe formé de triangles qui soit suffisamment proche de la sphère. Les visiteurs de La Vilette à Paris ont pu remarquer l’effet remarquable obtenu par sa géode constituée de 6433 triangles. Le but de l’exercice consiste à utiliser l’ordinateur pour construire virtuellement une géode.
Mots-clés : géode, polyèdre, triangulation.
L’exercice s’inspire de plusieurs sites internet : La géode, Cabri dans l’espace de C. Camalon et Géode chez Wikipedia.
La construction des coupoles géodésiques a été particulièrement développée par l’architecte américain Richard Buckminster Fuller. L’une de ses géodes les plus remarquables est un dôme géodésique transparent de 80 m de diamètre qui fut construit sur l’île Sainte-Hélène à Montréal en 1967 pour être le pavillon des États-Unis à l’exposition universelle de Montréal et qui abrite aujourd’hui la « Biosphère ».
On comprend la difficulté de construire une sphère en essayant d’aplatir une orange. On peut se consoler en construisant un polyèdre suffisamment proche d’une sphère. Une des structures les plus simples et les plus solides est le triangle. On cherche donc généralement à construire un polyèdre formé uniquement de faces triangulaires tout en minimisant l’écart entre le volume de la sphère et celui du polyèdre.
La Géode de La Vilette est la première sphère parfaite que l’on a su construire. Les 6433 triangles de la peau extérieure sont galbés pour que l’ensemble soit réellement sphérique et réfléchisse tout le paysage. L’ingénieur G. Chamayou a construit la sphère de la géode à la demande de l’architecte de la Cité, A. Fainsilber, qui voulait y abriter la salle de cinéma hémisphérique. La figure géométrique de base est un icosaèdre à vingt faces triangulaires. Chacune des faces a été divisée en cent triangles plus petits de 0.80 à 1.20 mètre de côté. Cette structure primaire en triangles, l’ossature géodésique, a été construite en tubes d’acier. Sur celle-ci se superposent plusieurs couches, qui assurent l’isolation thermique, phonique et l’étanchéité. En dernier lieu, les 6433 triangles en acier inoxydable poli sont vissés sur une structure secondaire. En fait on a partagé les faces triangulaires de l’icosaèdre en cent petits triangles équilatéraux. Ceux-ci furent ensuite projetés sur la sphère circonscrite. Chacun des deux milles triangles fut ensuite partagé en quatre triangles également projetés sur la sphère circonscrite. La géode devrait alors être formée de huit mille faces triangulaires mais il ne faut pas tenir compte de la base qui permet de faire reposer la géode sur le sol. On apprend qu’il n’y a officiellement « que » 6433 triangles.
La plupart du temps, on part d’un icosaèdre, polyèdre régulier à vingt faces triangulaires (on peut construire des géodes à partir de n’importe quel polyèdre régulier à faces triangulaires, donc également à partir du tétraèdre et de l’octaèdre). Chaque face de l’icosaèdre est un triangle équilatéral que l’on va subdiviser en triangles plus petits. Ces triangles vont ensuite être projetés sur la sphère circonscrite à l’icosaèdre. On diminue ainsi de façon évidente l’écart entre le volume du nouveau polyèdre obtenu par triangulation et celui de la sphère.
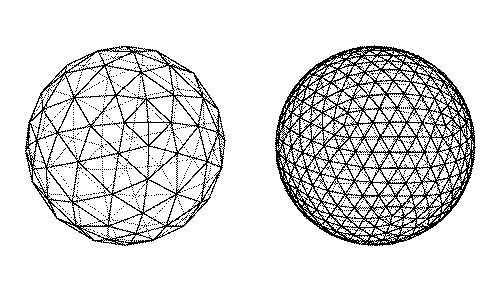
Plus le nombre de divisions est grand, plus l’impression d’obtenir une sphère est grand. On peut également concevoir des géodes en nid d’abeilles en prenant le polyèdre dual de la géode obtenue par triangulation (le polyèdre dual est obtenu en prenant les centres de chaque face puis en reliant ces sommets suivant leur appartenance aux faces originales contiguës ; on les projette également sur la sphère circonscrite).

En observant de près une géode en nid d’abeille, on constate qu’elle est constituée essentiellement d’hexagones. En la détaillant de plus près, on remarque que parmi ces hexagones se cachent douze pentagones correspondant aux sommets de l’icosaèdre. Il est en effet impossible de recouvrir une sphère en n’utilisant que des hexagones et, plus surprenant encore, il y a toujours exactement douze pentagones.

Le but de l’exercice est de permettre de représenter graphiquement des géodes à faces triangulaires et des géodes duales avec un découpage quelconque pour autant que la mémoire le permette.
La construction de l’icosaèdre est expliquée à plusieurs reprises sur le site. On part donc du principe que l’on est capable de représenter un icosaèdre.
La méthode la plus simple consiste à diviser une face de l’icosaèdre en n2 petits triangles équilatéraux identiques : on divise chaque côté du triangle initial en n parties égales, puis on mène par les points construits des parallèles à chaque côté.
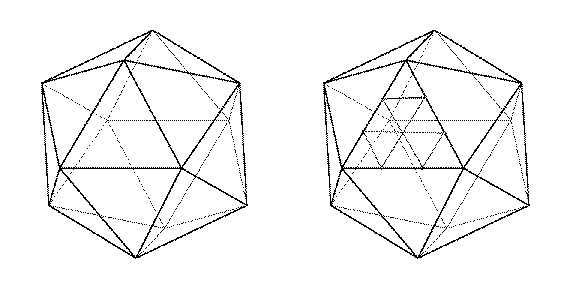
On projette ensuite les sommets des petits triangles sur la sphère (projection de centre le centre de la sphère). On peut alors remplacer une face de l’icosaèdre par les n2 faces triangulaires obtenues.
On recommence de même pour les autres faces de l’icosaèdre. C’est ainsi que l’on obtient une géode de 20n2 faces.
Pour construire la géode duale, il faut déterminer sur la sphère le centre de chacun des petits triangles et si les points centraux ainsi obtenus correspondent à des faces adjacentes de la géode normale, on doit joindre deux à deux ces sommets pour former les arêtes de la géode duale. Ces arêtes servent à définir les polygones des faces de la géode duale ; ce sont des hexagones, sauf douze d’entre elles qui sont des pentagones réguliers.
On peut définir une géode à partir de deux paramètres : un numéro N indiquant le type de polyèdre initial (N = 3 pour le tétraèdre, N = 4 pour l’octaèdre et N = 5 pour l’icosaèdre) et un nombre n indiquant le nombre de divisions le long de l’arête. On peut alors calculer le nombre de faces f du polygone régulier générateur ainsi que la densité D de la division des faces :
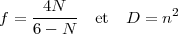
On obtient pour les géodes normales le nombre de faces F, le nombre d’arêtes A et le nombre de sommets S :
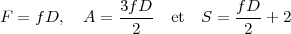
Dans le cas des géodes duales :
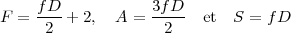
Les faces des géodes normales sont toutes des triangles tandis que leurs sommets sont d’ordre six et N. Les sommets des géodes duales sont tous d’ordre 3 tandis que leurs faces sont des hexagones et d’ordre N.
La solution actuellement proposée est donnée en Java : GeodeApplet.java, PolyLabPanel.java, Polyedre.java, UtilPolyedre.java et PrintUtilities.java. L’applet compilée peut être testée ci-dessous :