Résumé : un arbre est un objet qui peut être défini mathématiquement. Sur la base de déplacements très simples combinés à volonté, il est possible de représenter de nombreuses courbes, dont des plantes très ressemblantes à la réalité.
Mots-clés : grammaire, fractal, trigonométrie.
En 1968 le biologiste Aristid Lindemayer inventa un formalisme permettant la description de la croissance des plantes utilisable sur des ordinateurs. Cette description porte le nom de L-systems.
Pour commencer, considérons une algue bleu-vert appelée anabaena catenula. L’algue croît en filaments sous forme de chaînes de cellules. Il y a deux types de cellules : les cellules spécialisées qui ne se divisent pas et des cellules non-spécialisées qui se divisent et sont responsables de la croissance de l’algue. En laboratoire les cellules se divisent chaque quatorze heures environ. La division est asymétrique dans le sens où un descendant est généralement plus petit que l’autre au moment de la division. De plus, la division est gouvernée par une règle simple : si une cellule se présente comme un descendant gauche d’une division, alors sa progéniture gauche sera plus petite à la génération suivante. De même, à droite la progéniture sera plus petite à droite.
Le schéma ci-dessous donne un exemple :
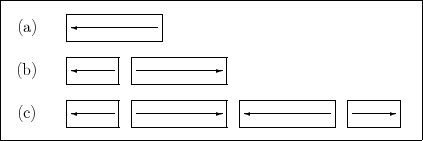
En (a) une grande cellule est montrée avec une flèche à gauche indiquant qu’elle est une cellule fille gauche. En (b) la cellule se divise en deux cellules : une petite à gauche et une grande à droite. En (c) il y a une nouvelle division et quatre cellules.
On peut écrire les règles de reproduction à l’aide d’une notation plus formelle : une chaîne de cellules est représentée par une chaîne de symboles :
Les règles de reproduction deviennent alors :
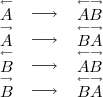
Par exemple, si on part de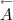 
, alors à l’étape suivante on a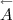 
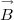puis
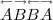
à la prochaine division cellulaire on a huit cellules :
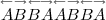
puis seize :
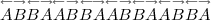
et ainsi de suite.
On peut utiliser le concept de la tortue de Seymour Papert pour interpréter graphiquement les L-systems. Imaginons une tortue se déplaçant sur une feuille de papier avec un crayon fixé à la patte. La tortue réagit à ces commandes symbolisées par les symboles suivants :
Un programme informatique doit permettre d’implémenter graphiquement les L-systems. L’utilisateur devra pouvoir introduire des chaînes à interpréter respectant les règles énoncées ci-dessus. En particulier, le flocon de Koch, le triangle de Sierpińsky, la courbe du dragon,...
On dira que la tortue est dans un état donné par sa position actuelle, sous forme de deux coordonnées x et y, et une direction actuelle spécifiée par un angle α. On l’écrit comme un triplet (x,y,α). L’état de la tortue est modifié chaque fois qu’une commande est interprétée. Un peu de trigonométrie élémentaire permet de déduire que :
l indique la longueur du pas et δ l’angle de rotation (à droite ou à gauche). La position de départ est toujours (0,0,0), c’est-à-dire que la tortue est tournée vers la droite. Pour simplifier, on utilise également des symboles représentant de petites courbes :
Des fractales classiques peuvent être construites à partir des L-systems. Le flocon de Koch peut être décrit comme suit :
| (1,1)L-system : | (1,2)flocon de Koch |
| (2,1)Axiome : | (2,2)F |
| (3,1)Règles de production : | (3,2)F-→F + F --F + F |
| (4,1)Paramètre : | (4,2)δ = 60 degrés |
On considére que la longueur du pas l est réduite de moitié à chaque étape de substitution1 .
La flèche de Sierpińsky peut être dessinée suivant le modèle :
| (1,1)L-system : | (1,2)flèche de Sierpińsky |
| (2,1)Axiome : | (2,2)L |
| (3,1)Règles de production : | (3,2)L-→ + R - L - R+ |
| (4,1) | (4,2)R-→- L + R + L- |
| (5,1)Paramètre : | (5,2)δ = 60 degrés |
| (1,1)L-system : | (1,2)courbe de Peano |
| (2,1)Axiome : | (2,2)F |
| (3,1)Règles de production : | (3,2)F-→FF + F + F + FF + F + F - F |
| (4,1)Paramètre : | (4,2)δ = 90 degrés |
Pour représenter un arbre, on peut procéder de la même façon. Il faut toutefois conserver la position de la tortue aux embranchements. On utilise alors les symboles [ pour sauver l’état actuel de la tortue et ] pour rétablir l’état sauvé.
| (1,1)L-system : | (1,2)un arbre |
| (2,1)Axiome : | (2,2)F |
| (3,1)Règles de production : | (3,2)F-→F![[+F ]](am57x.png) ![[- F ]](am58x.png) |
| (4,1)Paramètre : | (4,2)δ = 45 degrés pour + |
| (5,1) | (5,2)δ = 30 degrés pour - |
ou encore :
| (1,1)L-system : | (1,2)un arbre |
| (2,1)Axiome : | (2,2)F |
| (3,1)Règles de production : | (3,2)F-→FF -![[- F + F + F]](am59x.png) + ![[+F - F - F ]](am60x.png) |
| (4,1)Paramètre : | (4,2)δ = 22.5 degrés pour + |
| (5,1) | (5,2)δ = 22.5 degrés pour - |
et enfin :
| (1,1)L-system : | (1,2)un arbre |
| (2,1)Axiome : | (2,2)F |
| (3,1)Règles de production : | (3,2)F-→F![[+F ]](am61x.png) F![[- F]](am62x.png) ![[F ]](am63x.png) |
| (4,1)Paramètre : | (4,2)δ = 20 degrés pour + |
| (5,1) | (5,2)δ = 20 degrés pour - |
Les solutions sont en cours de développement... Toute solution est la bienvenue.