Résumé : la spirale est une courbe mathématique classique vieille comme le monde. Elle dispose de propriétés qui ont de tout temps fasciné les mathématiciens. En particulier, quelle est la longueur d’une spirale ? La réponse n’est peut-être pas évidente.
Mots-clés : trigonométrie, logarithme, intégration, récurrence.
En 1967 Benoît B. Mandelbrot se posait la question : How long is the coast of Britain1 ? Même si cette question paraît dénuée d’intérêt, elle est à la base des réflexions sur la théorie des fractales. La question fondamentale consiste à se demander si la longueur d’une telle courbe est finie ou infinie.
Sans vouloir répondre immédiatement à cette question délicate, on s’intéresse, dans cet exercice, à la mesure de la longueur des spirales. A première vue, les spirales peuvent être représentées sur une feuille de papier et ont une longueur infinie. Mais, ont-elles réellement une longueur infinie ?
Les spirales ont fasciné les mathématiciens de tout temps. Archimède (287-212 avant J.C.) écrivit un traité sur les spirales dont l’une porte son nom. La spirale d’Archimède est un bon modèle pour la piste d’un disque ou l’enroulement d’un tapis. La caractéristique principale de la spirale d’Archimède consiste à ce que la distance entre chaque révolution reste constante.
En passant aux coordonnées polaires, on peut trouver facilement l’équation de la spirale d’Archimède :
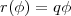
En remplaçant r(φ) par log r(φ) on obtient l’équation de la spirale logarithmique : log r(φ) = qφ ou encore
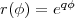
Le grand mathématicien suisse Jacob Bernoulli (1654-1705) consacra un traité, Spira Mirabilis, à la spirale logarithmique. Il fut tellement impressionné par elle qu’il choisit comme épitaphe sur sa pierre tombale à la cathédrale de Bâle Eadem Mutata Resurgo2 .
La propriété qui intéressait le plus Bernoulli était qu’une homothétie (avec pour centre le centre de la spirale) avait le même effet qu’une rotation.
Pour calculer la longueur de la spirale, on commence par calculer la longueur d’une spirale encore plus simple, la spirale polygonale. Elle est construite en prenant un segment de longueur a1 tracé verticalement de bas en haut. Ensuite on effectue une rotation à droite, on trace un segment de longueur a1 à nouveau de gauche à droite, puis un segment de longueur a2 dans la même direction. On poursuit ensuite ce principe avec a3, a4, etc. A titre d’exemple, on peut choisir succesivement ak = qk-1 et ak = 1∕k.
Une spirale plus lisse peut être obtenue facilement à l’aide de cette même construction. Chaque paire de segments aiai circonscrit un quart de cercle dont la longueur peut être facilement calculée.
Une spirale particulière porte le nom de spirale d’or ; on prend dans ce cas :
ak = 1∕gk-1 où g = (1 + 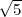 )∕2.
)∕2.
L’exercice consiste à représenter toutes les spirales mentionnées ci-dessus et à calculer la longueur de chacune d’elles ainsi que les rayons des points situés à angle fixe. Pour calculer la longueur de la frontière suisse, on prendra un fichier de données contenant les coordonnées de certains points qui lui appartiennent. Les conclusions sur les calculs des longueurs des spirales serviront à argumenter les conclusions sur le calcul de la longueur de la frontière suisse.
Ce problème est tiré de Chaos and Fractals de Peitgen, Jürgens et Saupe, Springer-Verlag, New-York, 1992 et de Les objets fractals de Benoît Mandelbrot, Flammarion, Paris, 1984.
Pour représenter la spirale d’Archimède, il est conseillé de passer en coordonnées polaires. Pour calculer les rayons de la spirale, il est conseillé de choisir un angle α et d’observer la suite des nombres représentant les rayons. La différence entre deux rayons rappelle une notion mathématique connue (aussi bien pour la spirale d’Archimède que pour la spirale logarithmique).
Pour démontrer la propriété découverte par Jacob Bernouilli, il suffit d’effectuer une rotation de la spirale et de déterminer le changement d’échelle correspondant. Graphiquement, cette propriété est aisément visualisable.
Pour calculer la longueur des spirales, il est conseillé de prendre des segments de droite spour commencer, puis des arcs de cercle inscrits dans ces segments. Bien qu’une approximation numérique puisse être faite simplement à l’aide de l’ordinateur, des simplifications faisant appel à des notions mathématiques simples peuvent également être utilisées (voir séries géométiques).
Les solutions sont en cours de développement... Toute solution est la bienvenue.