Résumé : y-a-t-il un logique dans le chaos ? C’est en s’intéressant à cette question que la résolution du problème dit du boulanger peut être utile. En réalité, la question est très simple : un boulanger prend un flan de pâte carré ; il l’aplatit en lui donnant la forme d’un rectangle, puis on prend la moitié de droite pour la replacer au-dessus de la moitié de gauche. On reforme ainsi un nouveau carré et on recommence (quelle belle pâte feuilletée). Supposons qu’une souris se soit trouvée prise dans la pâte, on peut se poser le problème suivant : où se trouvera la queue de la souris au bout de dix coups ?
Mots-clés : chaos, mélange, ergodicité, transformation périodique, récurrence.
L’exercice s’inspire de l’article Le chaos, puissance et impuissance par Simon Diner, directeur de recherche au CNRS, Revue du Palais de la découverte, Vol.24,No234, janvier 1996.
Si le chaos fait actuellement tellement de « bruit », c’est parce qu’il n’est nullement simplement anecdotique mais revêt au contraire l’aspect d’un événement historique : le passage d’une physique qui ne considérait que les phénomènes linéaires à une physique qui a décidé de regarder de près les phénomènes non linéaires. Ce passage a eu lieu au XXe siècle et pour une bonne part est à son début.
Le chaos mélange les genres. On pourrait penser qu’au-delà d’une certaine limite, il n’y a plus d’intérêt à observer un comportement chaotique. En fait on aurait tort car, parfois, on voit resurgir tout d’un coup des phénomènes périodiques, mélangés en quelque sorte à des phénomènres chaotiques. Apparaissent ce que les mathématiciens appellent des fenêtres périodiques.
Plusieurs transformations de ce type ont été très étudiées dans l’histoire du chaos, telle par exemple la transformation dite du boulanger :
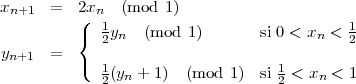
Ce sont toujours des petites récurrences qui interviennent, cette fois-ci dans le plan. Cette transformation part d’un carré de côté a (un flan de pâte carrée par exemple). On aplatit ce carré en lui donnant la forme d’un rectangle de côtés a∕2 et 2a, puis on coupe le rectangle en deux et on prend la moitié de droite pour le replacer au-dessus de la moitié de gauche. On reforme ainsi un nouveau carré et on recommence. Supposons qu’une souris se soit trouvée prise dans la pâte, on peut se poser le problème suivant : où se trouvera la queue de la souris au bout de dix coups ? Le problème n’est pas simple du tout ; si on veut savoir où est cette queue de souris au bout de dix coups, il faut faire effectivement les dix coups ; il n’existe aucune formule qui nous dise exactement où est la queue de la souris au bout des dix coups et ceci parce que la transformation-là engendre le chaos. Elle engendre une suite d’états qui possède une propriété très particulière appelée le mélange. C’est la première propriété chaotique. Elle est plus forte que la propriété ergodique. Si l’on examine ce qui arrive au demi carré inférieur initial, on voit que cette zone se fragmente de plus en plus en petits morceaux par petites bandes et envahit tout le carré en se mélangeant.
Prenons deux exemples. Dans la figure ci-dessous, la transformation est ergodique, cela veut dire que si on part d’un petit carré et qu’on regarde ce qui lui advient, on le voit parcourir toute la région avec application et sans jamais exploser : c’est là un comportement ergodique. Si maintenant cette transformation a une propriété de plus, celle d’être mélangeante, alors le même petit carré s’étale de plus en plus et couvre effectivement toute la surface en désordre (fig. ci-dessous). Il s’agit là de la première propriété du chaos, il en existera bien d’autres dans cette hiérarchie chaotique.
Cette propriété de mélange est une propriété essentielle, c’est elle qui assure qu’au cours de l’évolution le phénomène perd la mémoire. Il se décorrèle, au fur et à mesure que le temps passe. Il y a de moins en moins de relation avec ce que le phénomène était aux instants antérieurs. En fait, pour être exact, il faut dire qu’il perd une certaine mémoire. Il garde une grosse mémoire parce qu’il est déterministe et qu’à court terme, tout s’enchaîne avec une mécanique inexorable. Mais plus on s’éloigne dans le temps et moins les phénomènes sont reliés les uns aux autres.
Voici encore un exemple de transformation un peu analogue à celle du boulanger que l’on fait subir à une image :
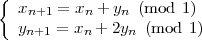
Cette transformation est bien mélangeante. Cet exemple montre la quintessence des surprises qui nous attendent dans le non-linéaire. Rien n’est jamais joué, il faut attendre jusqu’au bout et c’est à cause de cela qu’il y a une extraordinaire différence entre voir des phénomènes chaotiques sur ordinateur par calculs et observations expérimentales et démontrer qu’un phénomène a certaines propriétés chaotiques ou n’en a pas.
Le but du problème consiste donc à effectuer la transformation du boulanger sur un carré unitaire avec sa représentation. Il sera alors aisé de répondre à la question sur la queue de la souris. Dans un deuxième temps, il faudra décrire le comportement de la variante de la transformation du boulanger sur une image quelconque : découverte de cycles, mélange, etc.
Il est conseillé d’effectuer les transformations du boulanger sur un carré représenté par de nombreux points. La droite représentant la queue de la souris devra également être donnée sous forme de plusieurs points. Il est conseillé de prendre les coordonnées entre 0 et 1.
La formule (modulo 1) indique que l’on prend le reste de la division par 1. Soit dans le cas des nombres réels, la partie décimale. On peut travailler avec des entiers et utiliser (mod n).
Pour travailler sur une image, on considérera que celle-ci est donnée sous la forme d’une matrice de points dont les coordonnées entières représentent un point à l’écran (pixel). La valeur correspondante dans la matrice est un indice sur la couleur du point. Un deuxième paramètre doit donc définir également la palette des couleurs utilisées.
Les solutions sont en cours de développement... Toute solution est la bienvenue.