Résumé : comment représenter la terre vue de l’extérieur ? La réponse consiste, notamment, à projeter la sphère terrestre sur un plan en représentant le contour des continents, les méridiens et les parallèles.
Mots-clés : trigonométrie, coordonnées sphériques, projection.
Quelle vue de la terre a-t-on lorsqu’on l’observe depuis la navette spatiale ? Cette image, tout le monde la vue mais, comment l’obtient-on ?
En simplifiant, on peut considérer qu’il s’agit d’une projection orthogonale de la sphère terrestre sur un plan. De la même façon que l’on fait tourner une mappemonde, la représentation de la terre devra pouvoir être faite depuis n’importe quel point de vue, exprimé en termes de latitudes et longitudes. On doit pouvoir choisir la représentation des méridiens et des parallèles, permettre la transparence ou la détermination des parties cachées.
Pour commencer, il est conseillé de savoir représenter une sphère. Pour le faire, il est bon de rappeler le passage des coordonnées sphériques aux coordonnées cartésiennes :
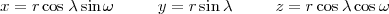
Pour placer la sphère terrestre dans la position souhaitée afin de projeter sur le plan Π la zone à représenter, on peut faire tourner la sphère sur elle-même d’un angle φ autour de l’axe Oz ; on peut également la basculer d’un angle α autour de l’axe Oy ; enfin, à la position obtenue par composition des deux rotations précédentes s’ajoute encore, à volonté, une rotation d’angle -β autour de l’axe Oz. Les matrices de rotation sont données ci-dessous :
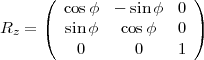
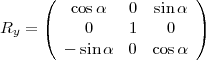
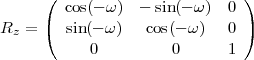
Le plan de projection Π est perpendiculaire à l’axe Ox. Pour savoir si un point est visible ou pas, il suffit d’observer le signe de x.
Les données pour représenter les continents peuvent être obtenues auprès du National Geophysical Data Center, NOAA, US Departement of Commerce under data announcement 88-MGG-02.
La solution actuellement proposée est donnée par les fichiers MatLab : MondeDemo.m, monde.m, Amerique.m, Europe.m, Iles.m, Pacifique.m, aidefun.m, param.m, spher2cart.m, deg2rad.m, continent.m et dessine.m.