Chapitre 25
L’aiguille de Buffon

Résumé : Buffon, naturaliste français, a entrepris une expérience étonnante. Il a jeté des aiguilles sur un parquet constitué de lames parallèles puis, il a comptabilisé le nombre de fois où les aiguilles sont tombées à cheval sur deux lames. Le résultat est étonnant. Les ordinateurs permettent aujourd’hui d’automatiser cette expérience fastidieuse.

Mots-clés : nombre aléatoire, hasard, probabilité.

Enoncé

Ce problème est tiré du supplément au Petit Archimède N^∘ 64-65, intitulé π, 1980. Le paragraphe consacré à l’aiguille de Buffon est très instructif et mérite une reproduction quasi complète.

Georges Louis Leclerc, comte de Buffon (1707-1788) est connu essentiellement pour son oeuvre de naturaliste. L’Histoire naturelle générale et particulière (15 volumes), l’Histoire naturelle des oiseaux (9 volumes), le Supplément à l’histoire naturelle (7 volumes), l’Histoire naturelle des minéraux et traité de l’aimant (5 volumes) lui vaudront la plus grande célébrité. Georges Louis Leclerc deviendra, par la grâce de Louis XV, comte de Buffon. Cet excellent administrateur (Buffon enrichira et agrandira le jardin du Roi), membre de l’Académie Française et de toutes les grandes académies européennes, fut aussi philosophe et mathématicien.

Ses œuvres mathématiques comprennent :

• une traduction de la Méthode des fluxions et des suites infinies de Newton, augmentée d’une Préface de 26 pages ;
• trois notes critiquant une proposition de Clairaut visant à ajouter au terme en 1∕x² de l’attraction de Newton un terme en 1∕x⁴ ;
• Des probabilités de la durée de la vie (175 pages) ;
• Etat général des naissances, des mariages et des morts.

C’est dans son Essai d’arithmétique morale publié en 1777 que l’on peut trouver le Mémoire sur le jeu de franc carreau qui contient le fameux problème de l’aiguille si souvent cité et pourtant si peu lu...

S’interrogera-t-on sur le plus grand plaisir rencontré en découvrant ce texte : vient-il du ton, du style de l’auteur ou bien de la démarche mathématique, de l’évantail des cas étudiés ? Nous ne saurions, quant à nous, le dire. Mais laissons la parole à M. de Buffon.

« L’Analyse est le seul instrument dont on se soit servi jusqu’à ce jour dans la science des probabilités, pour déterminer et fixer les rapports du hasard ; la Géométrie paraissait peu propre à un ouvrage aussi délié ; cependant si l’on y regarde de près, il sera facile de reconnaître que cet avantage de l’Analyse sur la Géométrie est tout à fait accidentel, et que le hasard selon qu’il est modifié et conditionné, se trouve du ressort de la géométrie aussi bien que celui de l’analyse ; pour s’en assurer, il suffira de faire attention que les jeux et les questions de conjecture ne roulent ordinairement que sur les rapports de quantités discrètes ; l’esprit humain plus familier avec les nombres qu’avec les mesures de l’étendue les a toujours préférés ; les jeux en sont une preuve, car leurs lois sont une arithmétique continuelle ; pour mettre donc la Géométrie en possession de ses droits sur la science du hasard, il ne s’agit que d’inventer des jeux qui roulent sur l’étendue et sur ses rapports, ou calculer le petit nombre de ceux de cette nature qui sont déjà trouvés ; le jeu du franc-carreau peut nous servir d’exemple : voici ses conditions qui sont fort simples.

» Dans une chambre parquetée ou pavée de carreaux égaux, d’une figure quelconque, on jette en l’air un écu ; l’un des joueurs parie que cet écu après sa chute se trouvera à franc-carreau, c’est-à-dire sur un seul carreau ; le second parie que cet écu se trouvera sur deux carreaux, c’est-à-dire qu’il couvrira un des joints qui les séparent ; un troisième joueur parie que l’écu se trouvera sur deux joints : on demande le sort de chacun de ces joueurs.

» Je cherche d’abord le sort du premier joueur et du second : pour le trouver, j’inscris dans l’un des carreaux une figure semblable, éloignée des côtés du carreau, de la longueur du demi-diamètre de l’écu ; le sort du premier joueur sera à celui du second comme la superficie de la couronne circonscrite est à la superficie de la figure inscrite : cela peut se démontrer aisément, car tant que le centre de l’écu est dans la figure inscrite, cet écu ne peut être que sur un seul carreau, puisque par construction cette figure inscrite est partout éloignée du contour du carreau, d’une distance égale au rayon de l’écu ; et, au contraire, dès que le centre de l’écu tombe au dehors de la figure inscrite, l’écu est nécessairement sur deux ou plusieurs carreaux, puisque alors son rayon est plus grand que la distance du contour de cette figure inscrite ou contour du carreau ; or, tous les points où peut tomber ce centre de l’écu sont représentés dans le premier cas par la superficie de la couronne qui fait le reste du carreau ; donc le sort du premier joueur est au sort du second, comme cette première superficie est à la seconde : ainsi pour rendre égal le sort de ces deux joueurs, il faut que la superficie de la figure inscrite soit égale à celle de la couronne, ou, ce qui est la même chose, qu’elle soit la moitié de la surface totale du carreau.

» Je me suis amusé à en faire le calcul, et j’ai trouvé que pour jouer à jeu égal sur des carreaux carrés, le côté du carreau devait être au diamètre de l’écu, comme 1 : 1 -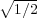 ; c’est-à-dire à peu près trois et demie fois plus grand que le diamètre de la pièce avec laquelle on joue.

» Pour jouer sur des carreaux triangulaires équilatéraux, le côté du carreau doit être au diamètre de la pièce, comme

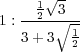
c’est-à-dire presque six fois plus grand que le diamètre de la pièce.

» Sur des carreaux en losange, le côté du carreau doit être au diamètre de la pièce, comme

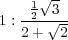
c’est-à-dire presque quatre fois plus grand.

» Enfin, sur des carreaux hexagones, le côté du carreau doit être au diamètre de la pièce, comme

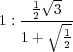
c’est-à-dire presque le double.

» Je n’ai pas fait le calcul pour d’autres figures, parce que celles-ci sont les seules dont on puisse remplir un espace sans y laisser des intervalles d’autres figures ; et je n’ai pas cru qu’il fût nécessaire d’avertir que les joints des carreaux ayant quelque largeur, ils donnent de l’avantage au joueur qui parie pour le joint, et que par conséquent l’on fera bien, pour rendre le jeu encore plus égal, de donner aux carreaux carrés un peu plus de trois et demie fois, aux triangulaires six fois, aux losanges quatre fois, et aux hexagones deux fois la longueur du diamètre de la pièce avec laquelle on joue.

» Je cherche maintenant le sort du troisième joueur qui parie que l’écu se trouvera sur deux joints ; et, pour le trouver, j’inscris dans l’un des carreaux une figure semblable, comme je l’ai déjà fait ; ensuite je prolonge les côtés de cette figure inscrite jusqu’à ce que qu’ils rencontrent ceux du carreau, le sort du troisième joueur sera à celui de son adversaire, comme la somme des espaces compris entre le prolongement de ces lignes et les côtés du carreau est au reste de la surface du carreau. Ceci n’a besoin, pour être pleinement démontré, que d’être bien entendu.

» J’ai fait aussi le calcul de ce cas, et j’ai trouvé que, pour jouer à jeu égal sur des carreaux carrés, le côté du carreau doit être au diamètre de la pièce, comme 1 : 1∕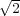, c’est-à-dire plus grand d’un peu moins d’un tiers.

» Sur des carreaux triangulaires équilatéraux, le côté du carreau doit être au diamètre de la pièce, comme 1 : 1∕2, c’est-à-dire le double.

» Sur des carreaux en losange, le côté du carreau doit être au diamètre de la pièce, comme

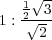
c’est-à-dire plus grand d’environ deux cinquièmes.

» Sur des carreaux hexagones, le côté du carreau doit être au diamètre de la pièce, comme 1 : 1∕2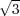, c’est-à-dire plus grand d’un demi-quart.

» Maintenant, le quatrième joueur parie que, sur des carreaux triangulaires équilatéraux, l’écu se trouvera sur six joints : que sur des carreaux carrés ou en losanges, il se trouvera sur quatre joints, et sur des carreaux hexagones, il se trouvera sur trois joints ; pour déterminer son sort, je décris de la pointe d’un angle de carreau, un cercle égal à l’écu, et je dis que sur des carreaux triangulaires équilatéraux, son sort sera à celui de son adversaire comme la moitié de la superficie de ce cercle est à celle du reste du carreau ; que sur des carreaux carrés ou en losanges, son sort sera à celui de l’autre comme la superficie entière du cercle est à celle du reste du carreau ; et que sur des carreaux hexagones, son sort sera à celui de son adversaire comme le double de la superficie du cercle est au reste du carreau. En supposant donc que la circonférence du cercle est au diamètre, comme 22 sont à 7 ; on trouvera que pour jouer à jeu égal sur des carreaux triangulaires équilatéraux, le côté du carreau doit être au diamètre de la pièce comme 1 : 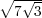∕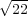, c’est-à-dire plus grand d’un peu plus d’un quart.

» Sur des carreaux en losange, le sort sera le même que sur des carreaux triangulaires équilatéraux.

» Sur des carreaux carrés, le côté du carreau coit être au diamètre de la pièce, comme 1 : 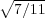, c’est-à-dire plus grand d’environ un cinquième.

» Sur des carreaux hexagones, le côté du carreau doit être au diamètre de la pièce, comme 1 : 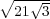∕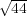, c’est-à-dire plus grand d’environ un troisième.

» J’omets ici la solution de plusieurs autres cas, comme lorsque l’un des joueurs parie que l’écu ne tombera que sur un joint ou sur deux, sur trois, etc. Ils n’ont rien de plus difficile que les précédents ; et d’ailleurs on joue rarement ce jeu avec d’autres conditions que celles dont nous avons fait mention.

» Mais si au lieu de jeter en l’aire une pièce ronde, comme un écu, on jetait une pièce d’une autre figure comme une pistole d’Espagne carrée, ou une aiguille, une baguette, etc., le problème demanderait un peu plus de géométrie, quoiqu’en général il fût toujours possible d’en donner la solution par des comparaisons d’espaces, comme nous allons le démontrer.

» Je suppose que dans une chambre, dont le parquet est simplement divisé par des joints parallèles, on jette en l’air une baguette, et que l’un des joueurs parie que la baguette ne croisera aucune des parallèles du parquet, et que l’autre au contraire parie que la baguette croisera quelques-unes de ces parallèles ; on demande le sort de ces deux joueurs. On peut jouer ce jeu sur un damier avec une aiguille à coudre ou une épingle sans tête.

Pour le trouver, je tire d’abord entre les deux joints parallèles AB et CD du parquet, deux autres lignes parallèles ab et cd, éloignées des premières de la moitié de la longueur de la baguette EF, et je vois évidemment que tant que le milieu de la baguette sera entre ces deux secondes parallèles, jamais elle ne pourra croiser les premières dans quelque situation EF, ef, qu’elle puisse trouver ; et comme tout ce qui peut arriver au-dessur de ab arrive de même au-dessous de cd, il ne s’agit que de déterminer l’un ou l’autre ; pour cela je remarque que toutes les situations de la baguette peuvent être représentées par le quart de la circonférence du cercle dont la longueur de la baguette est le diamètre ; appelant donc 2a la distance CA des joints du parquet, c le quart de la circonférence du cercle dont la longueur de la baguette est le diamètre, appelant 2b la longueur de la baguette, et f la longueur AB des joints, j’aurai f(a - b)c pour l’expression qui représente la probabilité de ne pas croiser le joint du parquet, ou ce qui est la même chose, pour l’expression de tous les cas où le milieu de la baguette tombe au-dessous de la ligne ab et au-dessus de la ligne cd.

» Mais lorsque le milieu de la baguette tombe hors de l’espace abcd, compris entre les secondes parallèles, elle peut, suivant sa situation, croiser ou ne pas croiser le joint ; de sorte que le milieu de la baguette étant, par exemple, en ε, l’arc φG représentera toutes les situations où elle croisera le joint, et l’arc GH toutes celles où elle ne le croisera pas, et comme il en sera de même de tous les points de la ligne εφ, j’appelle dx les petites parties de cette ligne, et y les arcs de cercle φG, et j’ai f(sydx) pour l’expression de tous les cas où la baguette croisera, et f(bc - sydx) pour celle des cas où elle ne croisera pas ; j’ajoute cette dernière expression à celle trouvée ci-dessus f(a - b)c, afin d’avoir la totalité des cas où la baguette ne croisera pas, et dès lors je vois que le sort du premier joueur est celui du second, comme ac - sydx : sydx.

» Si l’on veut donc que le jeu soit égal, l’on aura

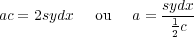
c’est-à-dire à l’aire d’une partie de la cycloïde dont le cercle générateur a pour diamètre 2b, longueur de la baguette ; or, on sait que cette aire de cycloïde est égale au carré du rayon, donc

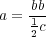
c’est-à-dire que la longueur de la baguette doit faire à peu près les trois quarts de la distance des joints du parquet.

» La solution de ce premier cas nous conduit aisément à celle d’un autre qui d’abord aurait paru plus difficile, qui est de déterminer le sort de ces deux joueurs dans une chambre pavée de carreaux carrés, car en inscrivant dans l’un des carreaux carrés un carré éloigné partout des côtés du carreau de la longueur b, l’on aura d’abord c(a - b)² pour l’expression d’une partie des cas où la baguette ne croisera pas le joint ; ensuite on trouvera (2a - b)sydx pour celle de tous les cas où elle croisera, et enfin cb(2a - b) -(2a - b)sydx pour le reste des cas où elle ne croisera pas ; ainsi le sort du premier joueur est à celui du second, comme

Si l’on veut donc que le jeu soit égal, l’on aura

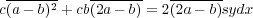
ou

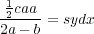
mais comme nous l’avons vu ci-dessus, sydx = bb ; donc

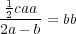
ainsi le côté du carreau doit être à la longueur de la baguette, à peu près comme 41∕22 : 1, c’est-à-dire pas tout à fait le double. Si l’on jouait donc sur un damier avec une aiguille dont la longueur serait la moitié de la longueur du côté des carrés du damier, il y aurait de l’avantage à parier que l’aiguille croisera les joints.

» On trouvera par un calcul semblable, que si l’on joue avec une pièce de monnaie carrée, la somme des sorts sera au sort du joueur qui parie pour le joint, comme aca : 4abb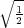 - b³ -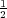Ab. A marque ici l’excès de la superficie du cercle circonscrit au carré, et b la demi-diagonale du carré.

» Ces exemples suffisent pour donner une idée des jeux que l’on peut imaginer sur les rapports de l’étendue. L’on pourrait se proposer plusieurs autres questions de cette espèce, qui ne laisseraient pas d’être curieuses et même utiles : si l’on demandait, par exemple, combien l’on risque à passer une rivière sur une planche plus ou moins étroite ; quelle doit être la peur que l’on doit avoir de la foudre ou de la chute d’une bombe, et nombre d’autres problèmes de conjecture, où l’on ne doit considérer que le rapport de l’étendue et qui, par conséquent, appartiennent à la géométrie tout autant qu’à l’analyse. »

Le problème consiste à reprendre cette expérience de manière moins fastidieuse que celle consistant à la vérifier en lançant une aiguille mais en utilisant les capacités des ordinateurs à générer des nombres aléatoires. C’est également l’occasion de tester les qualités du générateur de nombres aléatoires de l’ordinateur utilisé.

C’est dans la seconde partie du texte de Buffon que l’on trouve ce célèbre problème : il s’agit donc de lancer une aiguille (ou ‘baguette’) de longueur 2b sur un parquet formé de lames de largeur 2a et d’estimer la probabilité pour que l’aiguille coupe l’une des raies de ce parquet.

Indications

On voit que Buffon montre que les chances d’intersection ou non de l’aiguille avec une raie de parquet sont égales à

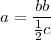
(c désignant le quart de la circonférence du cercle de rayon b). En d’autres termes, puisque c = π∕2b : La probabilité d’intersection est 1∕2 si a = 4b∕π. Il est aisé de voir que pour une longueur de l’aiguille égale à 2b (avec b ≤ a) la probabilité d’intersection est 2b∕πa.

En effet, si on réunit bout à bout deux aiguilles de longueurs respectives 2b₁ et 2b₂ (avec b₁ + b₂ ≤ a) on obtient une aiguille de longueur 2(b₁ + b₂) et cette aiguille coupera une raie si l’une des aiguilles composantes la coupe. Comme de plus la probabilité pour que les deux composantes coupent une raie (c’est-à-dire pour que le point de raccordement tombe juste sur cette raie) est nulle, il s’ensuit que la probabilité d’intersection de la grande aiguille est la somme des probabilités pour les aiguilles composantes.

Il résulte de ceci que la probabilité d’intersection pour une aiguille de longueur 2b (avec b ≤ a) est proportionnelle à la longueur de cette aiguille. Ainsi, en désignant par p(b) cette probabilité : p(b) = λb, et comme de plus on sait que p(b) = 1∕2 lorsque b = 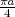on obtient immédiatement

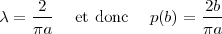
On peut faire d’autres démonstrations de ce cette égalité : ainsi, par exemple, désignons par y la distance du milieu I(0 ≤ y ≤ 2a) et par θ l’angle de l’aiguille et de la direction des raies (0 ≤ θ ≤).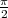

Il y aura intersection si y + bsinθ ≥ 2a ou y - bsinθ ≤ 0. C’est-à-dire si le point P(θ,y) appartient à la zone hachurée du graphique ci-dessous.

Or, la distribution uniforme ‘au hasard’ de y sur et θ sur entraîne que la probabilité cherchée est le rapport de l’aire de la surface hachurée à l’aire du rectangle × (représentant l’ensemble de tous les cas possibles). Ainsi, cette probabilité est

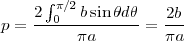
En particulier, si on prend une aiguille de longueur égale à la largeur des lames (b = a) la probabilité d’intersection est .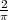

Si vous avez des trésors de patience, voici donc un moyen d’évaluer π : en lançant l’aiguille un très grand nombre de fois sur votre parquet en notant la fréquence relative d’intersections vous obtenez une évaluation de 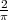. A l’ère des ordinateurs, il est possible de reprendre l’expérience de manière moins fastidieuse. Les jets d’aiguilles sont simulés en générant des couples (θ,y) de nombres ‘au hasard’ (0 ≤ θ ≤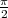,0 ≤ y ≤ 2) et on comptera une intersection si y + sinθ ≥ 2 ou y - sinθ ≤ 0 (c’est-à-dire en prenant a = b = 1).

Solutions

Les solutions sont en cours de développement... Toute solution est la bienvenue.