Résumé : un enfant tire derrière lui un jouet. Un joggeur est poursuivi par un chien. Le lien entre les deux histoires réside dans les trajectoires respectives des acteurs des scènes. Celles-ci peuvent être calculées en résolvant des équations différentielles.
Mots-clés : vecteur, équation différentielle, projection, produit scalaire, animation.
Un enfant se promène sur un plan. Sa trajectoire est donnée par deux fonctions du temps X(t) et Y (t). Supposons maintenant que l’enfant tire derrière lui un jouet, auquel il est relié par une barre rigide de longueur a. Quelle est la trajectoire du jouet quand l’enfant se déplace ?
Un joggeur court le long de sa piste préférée (piste plane) pour faire son exercice quotidien. Soudain, il est attaqué par un chien. Celui-ci se déplace à une vitesse constante w. Calculez et représentez la trajectoire du chien. Celle-ci a pour propriété que le chien s’oriente en tout temps vers son objectif : le joggeur. On considère que ce dernier se déplace sur une piste donnée et que son mouvement est décrit par deux fonctions du temps X(t) et Y (t).
On demande de représenter dans les deux cas les trajectoires obtenues. On pourra considérer comme chemin, par exemple pour l’enfant et le jouet, un cercle ou une fonction sinusoïdale : X(t) = t, Y (t) = 5sint. Pour le joggeur, on choisira un chemin rectiligne ou elliptique avec vitesses différentes pour le chien.
Cet exercice est extrait du livre Solving Problems in Scientific Computing Using Maple and Matlab de Walter Gander et Jiří Hřebíček chez Springer-Verlag, Berlin, 1993.
Ce problème fait appel à la résolution d’équations différentielles. Maple est un logiciel (comme Mathematica) qui permet de résoudre de manière formelle des équations différentielles. Ces résultats peuvent ensuite être traités par des logiciels plus orientés ‘applications numériques’, comme MATLAB. Les possibilités d’animation de ce dernier peuvent également être exploitées efficacement dans ce type de problème.
Les équations de la trajectoire du jouet par rapport à l’enfant peuvent être construites à partir du schéma ci-dessous.
La distance entre le point (X(t),Y (t)) et (x(t),y(t)) est la longueur de la barre. Donc
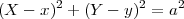
Le jouet se déplace toujours dans la direction de la barre. La vecteur qui relie l’enfant au jouet est donc un multiple du vecteur vitesse du jouet vJ = (ẋ,ẏ)T :
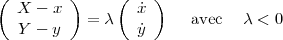
La valeur absolue de la vitesse du jouet dépend de la direction du vecteur de vitesse de l’enfant vE. D’après le schéma, on remarque que la valeur absolue de la vitesse du jouet est donnée par la valeur absolue de la projection du vecteur vitesse de l’enfant sur la barre. On déduit donc,
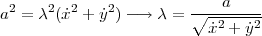
Donc,
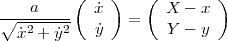
Pour calculer la vitesse du jouet, on normalise le vecteur (X - x,Y - y)T et on obtient un vecteur w de longueur un ; on détermine la projection de vE = (Ẋ,Ẏ)T sur le sous-espace vectoriel généré par w (il s’agit du produit scalaire vET w, puisque vET w = |vE||w|cosα et |w| = 1). Donc, vJ = (ẋ,ẏ)T = (vET w)w.
En MATLAB, la fonction ode45 permet la résolution numérique d’équations différentielles.
Pour le joggeur, on considère les équations suivantes. Le chien court à une vitesse constante :
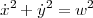
Le vecteur vitesse du chien est parallèle à la différence des positions :
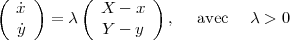
En substituant la première équation dans la deuxième, on a :
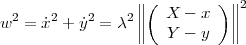
On peut résoudre pour λ :
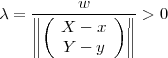
En substituant cette expression dans la deuxième équation, on obtient finalement :
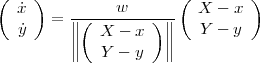
Les solutions sont en cours de développement... Toute solution est la bienvenue.