Résumé : comment se comporte une balle de tennis. La trajectoire est difficile à calculer car, il faut tenir compte de plusieurs forces. Cette trajectoire ne peut pas être obtenue analytiquement. Il faut donc passer par des approximations numériques.
Mots-clés : approximation, équation différentielle, trajectoire, force, fluide, accélération, frottement, effet Magnus.
Quelle est la trajectoire d’une balle de tennis ? Dans cet exercice, on souhaite
construire un modèle réaliste tenant compte de la masse m et du diamètre d de la
balle. La balle tournoie sur elle-même avec une vitesse angulaire 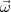 (le vecteur
(le vecteur 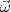 a
la direction de l’axe de rotation et comme longueur ω = dφ(t)∕dt =
a
la direction de l’axe de rotation et comme longueur ω = dφ(t)∕dt = 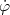 (t), où φ(t)
est l’angle de rotation).
(t), où φ(t)
est l’angle de rotation).
Comme modèle, on peut considérer un point doté d’une masse se déplaçant sous l’influence des forces suivantes :
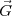 = m
= m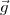 , où
, où 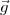 = (0,0,-g) est le vecteur de l’accélération dû
à la gravitation ;
= (0,0,-g) est le vecteur de l’accélération dû
à la gravitation ;
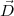 = -DL(v)
= -DL(v)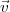 ∕v, dont la direction est opposée
à celle de
∕v, dont la direction est opposée
à celle de 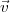 ;
;
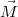 = ML
= ML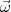 ∕ω×
∕ω×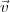 ∕v ; cette force est perpendiculaire
à
∕v ; cette force est perpendiculaire
à 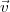 et
et 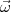 .
.Les grandeurs des forces de frottement DL et de Magnus ML sont données par la théorie des fluides :
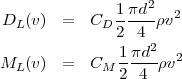
où ρ est la densité de l’air. Les coefficients CD et CM dépendent pour les fluides (air) de la vitesse v, la rotation de la balle et le matériel qui constitue sa surface. Ces coefficients sont obtenus expérimentalement.
Dans la littérature, on peut trouver que, pour une balle de tennis dont la
vitesse v 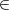
![[13.6,28]](am129x.png) m∕sec et dont le nombre de révolutions n
m∕sec et dont le nombre de révolutions n 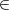
![[800,3250 ]](am130x.png) rpm
(révolutions à la minute), les coefficients CD et CM dépendent de v∕w seulement,
où w = d∕2 ⋅
rpm
(révolutions à la minute), les coefficients CD et CM dépendent de v∕w seulement,
où w = d∕2 ⋅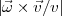 est en quelque sorte la projection de la vitesse équatoriale
ωd∕2 de la balle en rotation sur le vecteur vitesse
est en quelque sorte la projection de la vitesse équatoriale
ωd∕2 de la balle en rotation sur le vecteur vitesse 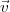 . Les expressions suivantes
sont alors obtenues :
. Les expressions suivantes
sont alors obtenues :
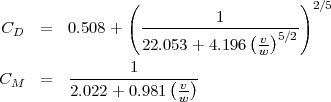
Pour une balle de tennis, on peut négliger la décélération de la révolution de la balle, donc w est constant.
La trajectoire de la balle est alors définie par les équations de Newton pour le
vecteur position 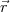 (t) :
(t) :
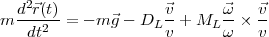
avec les conditions initiales
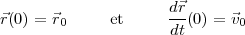
Cette équation est un système non linéaire de trois équations différentielles et aucune solution analytique n’existe pour elle, il faut donc la résoudre numériquement.
En pratique, le cas le plus fréquent est celui où la balle n’a pas d’effet, pour
lequel la vitesse angulaire reste dans un plan horizontal et perpendiculaire au
vecteur 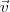 0 et donc, d’après l’équation ci-dessus, reste perpendiculaire
au vecteur
0 et donc, d’après l’équation ci-dessus, reste perpendiculaire
au vecteur 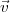 (t), pour t ≥ 0 ; de sorte la trajectoire reste dans un plan
vertical. Considérons l’axe x dans ce plan, l’équation ci-dessus devient
alors :
(t), pour t ≥ 0 ; de sorte la trajectoire reste dans un plan
vertical. Considérons l’axe x dans ce plan, l’équation ci-dessus devient
alors :
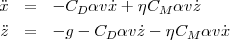
où v = 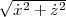 et α = (ρπd2)∕(8m). Le paramètre η = ±1 décrit la
direction de la rotation. Les conditions initiales pour t = 0 sont :
et α = (ρπd2)∕(8m). Le paramètre η = ±1 décrit la
direction de la rotation. Les conditions initiales pour t = 0 sont :
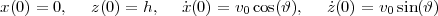
où v0 est la grandeur de la vitesse initiale 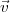 0 et ϑ est l’angle entre
0 et ϑ est l’angle entre 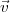 0 et l’axe
des x.
0 et l’axe
des x.
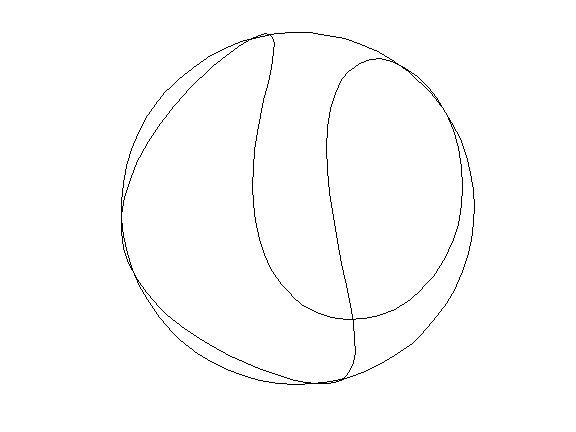
Pour tout savoir sur le tennis, on trouvera également ci-après les équations paramétriques permettant de représenter la couture d’une balle de tennis :
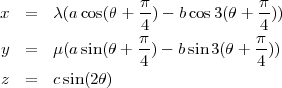
où
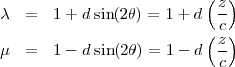
et le paramètre θ = 2πt, et 0 ≤ t ≤ 1.0. Si d = 0 et c2 = 4ab, alors la courbe est située sur une sphère de rayon a + b.
Le problème consiste donc a représenter le mouvement et la couture de la balle de tennis. Il est tiré de Mathematical Elements for Computer Graphics de David F. Rogers et J. Alan Adams chez McGraw-Hill, 1990 et de Solving Problems in Scientific Computing Using Maple and Matlab de Walter Gander et Jiří Hřebíček chez Springer-Verlag, Berlin, 1993.

En raison de la nature non linéraire du problème, il faut utiliser des méthodes numériques pour le résoudre. Pour résoudre un système de n équations différentielles avec conditions initiales
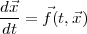
où 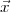 = (x1,x2,…,xn), on peut utiliser la fonction MatLab ode23 (ou ode45),
qui implémente une méthode optimisée de Runge-Kutta d’ordre 2 et 3
(respectivement 4 et 5).
= (x1,x2,…,xn), on peut utiliser la fonction MatLab ode23 (ou ode45),
qui implémente une méthode optimisée de Runge-Kutta d’ordre 2 et 3
(respectivement 4 et 5).
Il faut définir une fonction-m pour chaque modèle selon le schéma suivant :
function xdot=tennis(t,x)
xdot(1)= xdot(2)= xdot(3)= xdot(4)= |
où xdot(i) représente la i-ème équation différentielle. L’utilisation de ode23 se fait comme suit :
ode23(’tennis’,tmin,tmax,x);
|
où ’tennis’ indique le nom de la fonction-m, tmin et tmax les bornes de t et x est une matrice contenant les conditions initiales pour x(i).
La solution actuellement proposée est donnée par les fichiers MatLab : balleTennisDemo.m, balleTennisDemo.mat, balle_tennis.m et btennis.m.